Question and Answers Forum

AllQuestion and Answers: Page 1010

Question Number 118242 Answers: 1 Comments: 0

solve ∫_0 ^π ((xcosx)/((1+sin^2 x)))dx

$${solve} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{x}\mathrm{cos}{x}}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}\right)}{dx} \\ $$

Question Number 118239 Answers: 2 Comments: 0

Given that x,y,z are real numbers such that x+y+z=0 and xyz=−432. If a=(1/x)+(1/y)+(1/z), find the smallest possible value of a.

$$\mathrm{Given}\:\mathrm{that}\:{x},{y},{z}\:\mathrm{are}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that} \\ $$$${x}+{y}+{z}=\mathrm{0}\:\mathrm{and}\:{xyz}=−\mathrm{432}. \\ $$$$\mathrm{If}\:{a}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}},\:\mathrm{find}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{possible} \\ $$$$\mathrm{value}\:\mathrm{of}\:{a}. \\ $$

Question Number 118231 Answers: 1 Comments: 0

Given a matrix A= (((−1 3 2)),(( 0 1 4)),((−2 3 2)) ) and A^(−1) = (1/(10))(kA+9I−A^2 ). find k.

$${Given}\:{a}\:{matrix}\:{A}=\:\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{2}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{4}}\\{−\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$${and}\:{A}^{−\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{10}}\left({kA}+\mathrm{9}{I}−{A}^{\mathrm{2}} \right). \\ $$$${find}\:{k}. \\ $$

Question Number 118230 Answers: 1 Comments: 0

If ∫ ((((√x))^5 )/(((√x))^7 +x^6 )) dx = p ln ((x^q /(x^q +1))) + C find the value of p and q.

$$\mathrm{If}\:\int\:\frac{\left(\sqrt{\mathrm{x}}\right)^{\mathrm{5}} }{\left(\sqrt{\mathrm{x}}\right)^{\mathrm{7}} +\mathrm{x}^{\mathrm{6}} }\:\mathrm{dx}\:=\:\mathrm{p}\:\mathrm{ln}\:\left(\frac{\mathrm{x}^{\mathrm{q}} }{\mathrm{x}^{\mathrm{q}} +\mathrm{1}}\right)\:+\:\mathrm{C}\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}. \\ $$

Question Number 118228 Answers: 1 Comments: 0

lim_(x→0) ((Σ_(r=1) ^(10) (x+r)^(2020) )/((x^(1008) +1)(3x^(1012) +1))) =?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sum_{\mathrm{r}=\mathrm{1}} ^{\mathrm{10}} \left(\mathrm{x}+\mathrm{r}\right)^{\mathrm{2020}} }{\left(\mathrm{x}^{\mathrm{1008}} +\mathrm{1}\right)\left(\mathrm{3x}^{\mathrm{1012}} +\mathrm{1}\right)}\:=?\: \\ $$

Question Number 118227 Answers: 1 Comments: 0

If x = (√(42−(√(42−(√(42−...)))))) y = (√(x+(√(x+(√(x+...)))))) z=(√(y.(√(y.(√(y.(√(y...)))))))) . Find x+y+z .

$${If}\:{x}\:=\:\sqrt{\mathrm{42}−\sqrt{\mathrm{42}−\sqrt{\mathrm{42}−...}}} \\ $$$${y}\:=\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}} \\ $$$${z}=\sqrt{{y}.\sqrt{{y}.\sqrt{{y}.\sqrt{{y}...}}}}\:.\:{Find}\:{x}+{y}+{z}\:. \\ $$

Question Number 118218 Answers: 3 Comments: 0

∫ sin^6 (2x)dx =?

$$\:\int\:\mathrm{sin}\:^{\mathrm{6}} \left(\mathrm{2}{x}\right){dx}\:=?\: \\ $$

Question Number 118210 Answers: 1 Comments: 0

Question Number 118209 Answers: 1 Comments: 0

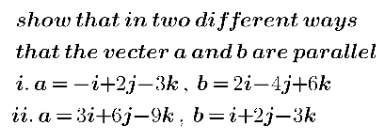
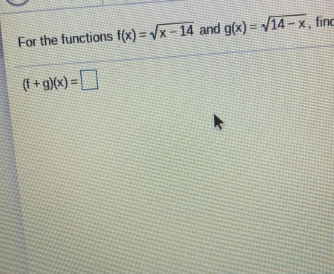
Question Number 118203 Answers: 2 Comments: 0

Question Number 118260 Answers: 3 Comments: 1

∫ ((x^2 −1)/(x^4 +x^2 +1)) dx

$$\int\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$

Question Number 118196 Answers: 1 Comments: 0

solve in N: b^3 (2b^2 +2b+1)=18360

$${solve}\:{in}\:\mathbb{N}: \\ $$$${b}^{\mathrm{3}} \left(\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\right)=\mathrm{18360} \\ $$

Question Number 118193 Answers: 1 Comments: 0

Given A=n^2 −2n+2 , B=n^2 +2n+2 n ∈ N^∗ −{1}. Show that ∀ divisor of A which divise n can also divise 2. Show that all common divisor of A and B can divise 4n.

$${Given}\:{A}={n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{2}\:,\:{B}={n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{2} \\ $$$${n}\:\in\:\mathbb{N}^{\ast} −\left\{\mathrm{1}\right\}. \\ $$$${Show}\:{that}\:\forall\:{divisor}\:{of}\:{A}\:{which}\:{divise} \\ $$$${n}\:{can}\:{also}\:{divise}\:\mathrm{2}. \\ $$$${Show}\:{that}\:{all}\:{common}\:{divisor}\:{of}\: \\ $$$${A}\:{and}\:{B}\:{can}\:{divise}\:\mathrm{4}{n}. \\ $$

Question Number 118189 Answers: 0 Comments: 0

Question Number 118188 Answers: 1 Comments: 2

Question Number 118184 Answers: 2 Comments: 1

factorise x^4 +4

$${factorise}\:{x}^{\mathrm{4}} +\mathrm{4} \\ $$

Question Number 118181 Answers: 1 Comments: 1

find all numbers >1 from N which their cube are <18360

$${find}\:{all}\:{numbers}\:>\mathrm{1}\:{from}\:\mathbb{N}\:{which} \\ $$$${their}\:{cube}\:{are}\:<\mathrm{18360} \\ $$

Question Number 118180 Answers: 1 Comments: 0

show that if n is odd , n(n^2 +3) is even.

$${show}\:{that}\:{if}\:{n}\:{is}\:{odd}\:,\:{n}\left({n}^{\mathrm{2}} +\mathrm{3}\right)\:{is}\:{even}. \\ $$

Question Number 118172 Answers: 1 Comments: 0

Find the area of a rhombus with side 8 cm

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{rhombus}\:\mathrm{with}\:\mathrm{side}\:\:\mathrm{8}\:\mathrm{cm} \\ $$

Question Number 118171 Answers: 0 Comments: 2

Question Number 118166 Answers: 1 Comments: 0

Question Number 118165 Answers: 2 Comments: 1

Question Number 118161 Answers: 2 Comments: 0

if p^→ =5i^ +λj^ −3k^ and q^ =i^ +3j^ −5k^ then find the value of λ so that p^→ +q^→ and p^→ −q^→ are perpendicular vectors

$${if}\:\overset{\rightarrow} {{p}}=\mathrm{5}\hat {{i}}+\lambda\hat {{j}}−\mathrm{3}\hat {{k}}\:{and}\:\hat {{q}}=\hat {{i}}+\mathrm{3}\hat {{j}}−\mathrm{5}\hat {{k}}\:{then}\:{find}\:{the}\:{value}\:{of}\:\lambda\:{so}\:{that}\:\overset{\rightarrow} {{p}}+\overset{\rightarrow} {{q}}\:{and}\:\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\:{are}\:{perpendicular}\:{vectors} \\ $$

Question Number 118156 Answers: 0 Comments: 2

(1−x^2 )y′′−8xy′−12y=0

$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}''−\mathrm{8}{xy}'−\mathrm{12}{y}=\mathrm{0} \\ $$

Question Number 118150 Answers: 2 Comments: 1

Determine all function f:R╲{0,1} →R satisfying the functional relation f(x)+f((1/(1−x))) = ((2(1−2x))/(x(1−x))); for x≠0 and x≠1

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{function}\:\mathrm{f}:\mathbb{R}\diagdown\left\{\mathrm{0},\mathrm{1}\right\}\:\rightarrow\mathbb{R} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{functional}\:\mathrm{relation} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2x}\right)}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)};\:\mathrm{for}\:\mathrm{x}\neq\mathrm{0}\:\mathrm{and}\:\mathrm{x}\neq\mathrm{1} \\ $$

Question Number 118145 Answers: 3 Comments: 1

∫ (dx/((x+1)^2 (x^2 +1))) ?

$$\int\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:? \\ $$

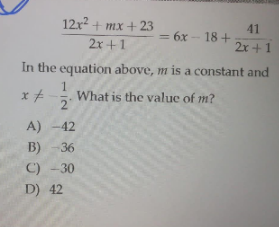
Pg 1005 Pg 1006 Pg 1007 Pg 1008 Pg 1009 Pg 1010 Pg 1011 Pg 1012 Pg 1013 Pg 1014

Contact: info@tinkutara.com