Question and Answers Forum

AllQuestion and Answers: Page 1006

Question Number 117543 Answers: 2 Comments: 0

If vector a^→ +b^→ +c^→ =0 ∣a^→ ∣=7, ∣b^→ ∣=3 and ∣c^→ ∣=5 find the angle vector a^→ and c^→ ?

$$\mathrm{If}\:\mathrm{vector}\:\overset{\rightarrow} {\mathrm{a}}+\overset{\rightarrow} {\mathrm{b}}+\overset{\rightarrow} {\mathrm{c}}=\mathrm{0} \\ $$$$\mid\overset{\rightarrow} {\mathrm{a}}\mid=\mathrm{7},\:\mid\overset{\rightarrow} {\mathrm{b}}\mid=\mathrm{3}\:\mathrm{and}\:\mid\overset{\rightarrow} {\mathrm{c}}\mid=\mathrm{5} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{vector}\:\overset{\rightarrow} {\mathrm{a}}\:\mathrm{and}\:\overset{\rightarrow} {\mathrm{c}}\:? \\ $$

Question Number 117527 Answers: 1 Comments: 0

∫_( 0) ^( 1) xsec(2x)dx

$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \mathrm{xsec}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$

Question Number 117518 Answers: 1 Comments: 0

f(x+1)+xf(1−x)=x^2 f^(−1) (x) =?

$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{xf}\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=? \\ $$

Question Number 117511 Answers: 3 Comments: 0

Question Number 117498 Answers: 3 Comments: 0

lim_(x→0) ((sin (x−sin x))/( (√(1+x^3 ))−1)) ?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }−\mathrm{1}}\:? \\ $$

Question Number 117500 Answers: 1 Comments: 0

In ΔABC, (a/(cos A))=(b/(cos B))=(c/(cos C)), then ΔABC is A. irregular sides acute-angled triangle B. obtuse-angled triangle C. right-angled triangle D. equilateral triangle E. isoceles triangle

$$\mathrm{In}\:\Delta\mathrm{ABC},\:\frac{{a}}{\mathrm{cos}\:{A}}=\frac{{b}}{\mathrm{cos}\:{B}}=\frac{{c}}{\mathrm{cos}\:{C}}, \\ $$$$\mathrm{then}\:\Delta\mathrm{ABC}\:\mathrm{is}\: \\ $$$${A}.\:\mathrm{irregular}\:\mathrm{sides}\:\mathrm{acute}-\mathrm{angled}\:\mathrm{triangle} \\ $$$${B}.\:\mathrm{obtuse}-\mathrm{angled}\:\mathrm{triangle} \\ $$$${C}.\:\mathrm{right}-\mathrm{angled}\:\mathrm{triangle} \\ $$$${D}.\:\mathrm{equilateral}\:\mathrm{triangle} \\ $$$${E}.\:\mathrm{isoceles}\:\mathrm{triangle} \\ $$

Question Number 117497 Answers: 1 Comments: 0

find the solution set of the equation sec 3θ = sec θ

$$\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{equation}\:\mathrm{sec}\:\mathrm{3}\theta\:=\:\mathrm{sec}\:\theta \\ $$

Question Number 117496 Answers: 2 Comments: 0

∫ ((sec^2 θ tan^2 θ)/( (√(9−tan^2 θ)))) dθ =?

$$\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta\:\mathrm{tan}\:^{\mathrm{2}} \theta}{\:\sqrt{\mathrm{9}−\mathrm{tan}\:^{\mathrm{2}} \theta}}\:\mathrm{d}\theta\:=? \\ $$

Question Number 117493 Answers: 1 Comments: 0

∫_c (3xy−e^(sin x) )dx+(7x+(√(y^4 +1)) )dy C : triangle with vertex (0,0),(0,1) and (1,0)

$$\int_{\mathrm{c}} \left(\mathrm{3xy}−\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \right)\mathrm{dx}+\left(\mathrm{7x}+\sqrt{\mathrm{y}^{\mathrm{4}} +\mathrm{1}}\:\right)\mathrm{dy} \\ $$$$\mathrm{C}\::\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{vertex}\:\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\mathrm{and}\:\left(\mathrm{1},\mathrm{0}\right) \\ $$

Question Number 117486 Answers: 1 Comments: 0

Question Number 117482 Answers: 2 Comments: 0

If cosec^(−1) x = cot^(−1) y, show that (d^2 y/dx^2 ) + (1/y^3 ) = 0

$$\:\mathrm{If}\:\:\mathrm{cosec}^{−\mathrm{1}} {x}\:\:=\:\:\mathrm{cot}^{−\mathrm{1}} {y},\:\mathrm{show}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:\:+\:\:\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\:\:=\:\:\mathrm{0} \\ $$

Question Number 117481 Answers: 2 Comments: 0

Question Number 117480 Answers: 1 Comments: 1

Question Number 117475 Answers: 1 Comments: 0

(6/5).((24)/(23)).((54)/(53)).((96)/(95)).((150)/(149)).((216)/(215)).((294)/(293))....

$$\frac{\mathrm{6}}{\mathrm{5}}.\frac{\mathrm{24}}{\mathrm{23}}.\frac{\mathrm{54}}{\mathrm{53}}.\frac{\mathrm{96}}{\mathrm{95}}.\frac{\mathrm{150}}{\mathrm{149}}.\frac{\mathrm{216}}{\mathrm{215}}.\frac{\mathrm{294}}{\mathrm{293}}.... \\ $$

Question Number 117470 Answers: 3 Comments: 5

(d/dx)sin^(−1) (((2x)/(1+x^2 ))) atx=1

$$\frac{{d}}{{dx}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{atx}=\mathrm{1} \\ $$

Question Number 117463 Answers: 0 Comments: 2

Question Number 117460 Answers: 0 Comments: 2

((2(√2))/(9801))Σ_(n=1) ^∞ (((4n)!(1103+26390n))/((n!)^4 396^(4n) ))=(1/π) (Prove that)

$$\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9801}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{4}{n}\right)!\left(\mathrm{1103}+\mathrm{26390}{n}\right)}{\left({n}!\right)^{\mathrm{4}} \mathrm{396}^{\mathrm{4}{n}} }=\frac{\mathrm{1}}{\pi}\:\:\:\left({Prove}\:{that}\right) \\ $$

Question Number 117458 Answers: 1 Comments: 0

(4/3).((16)/(15)).((36)/(35)).((64)/(63)).((100)/(99)).((144)/(143)).((196)/(195)).((256)/(255)).((324)/(323))......∞

$$\frac{\mathrm{4}}{\mathrm{3}}.\frac{\mathrm{16}}{\mathrm{15}}.\frac{\mathrm{36}}{\mathrm{35}}.\frac{\mathrm{64}}{\mathrm{63}}.\frac{\mathrm{100}}{\mathrm{99}}.\frac{\mathrm{144}}{\mathrm{143}}.\frac{\mathrm{196}}{\mathrm{195}}.\frac{\mathrm{256}}{\mathrm{255}}.\frac{\mathrm{324}}{\mathrm{323}}......\infty \\ $$

Question Number 117446 Answers: 2 Comments: 0

Evaluate ∫((3x^2 −5)/(x^4 +6x^2 +25))dx

$$\mathrm{Evaluate}\:\int\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}}{{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{25}}\mathrm{d}{x} \\ $$

Question Number 117439 Answers: 1 Comments: 0

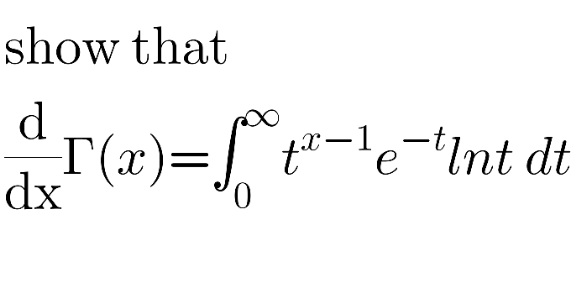
Question Number 117438 Answers: 4 Comments: 0

∫_(−∞) ^( ∞) cos((1/2)πx^2 )dx

$$ \\ $$$$\:\:\:\:\:\int_{−\infty} ^{\:\infty} \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\pi{x}^{\mathrm{2}} \right){dx}\:\:\:\:\: \\ $$$$ \\ $$

Question Number 117437 Answers: 2 Comments: 0

∫_0 ^∞ (dx/(a^3 +x^3 )) generaly ∫_0 ^∞ (dx/(p+x^n ))

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{a}^{\mathrm{3}} +{x}^{\mathrm{3}} } \\ $$$$ \\ $$$${generaly} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{p}+{x}^{{n}} } \\ $$

Question Number 117508 Answers: 1 Comments: 0

f(x+1)+f(x−1) = x^2 find f^(−1) (x) =?

$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)\:=\:\mathrm{x}^{\mathrm{2}} \: \\ $$$$\mathrm{find}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=? \\ $$

Question Number 117503 Answers: 1 Comments: 0

Question Number 117434 Answers: 0 Comments: 0

Question Number 117433 Answers: 0 Comments: 0

Pg 1001 Pg 1002 Pg 1003 Pg 1004 Pg 1005 Pg 1006 Pg 1007 Pg 1008 Pg 1009 Pg 1010

Contact: info@tinkutara.com