
AllQuestion and Answers: Page 1005
Question Number 119814 Answers: 3 Comments: 0
Question Number 119733 Answers: 1 Comments: 5
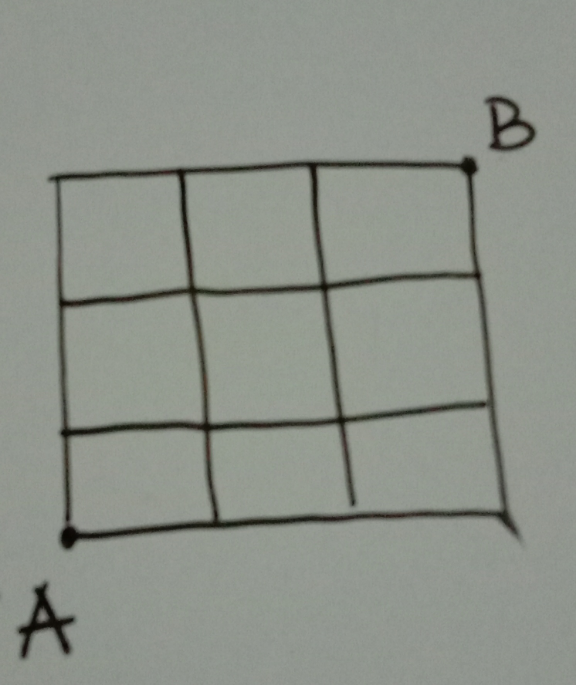
Question Number 119815 Answers: 1 Comments: 0
Question Number 119725 Answers: 3 Comments: 1
Question Number 119724 Answers: 2 Comments: 0
Question Number 119713 Answers: 1 Comments: 3
Question Number 119702 Answers: 0 Comments: 0

Question Number 119706 Answers: 0 Comments: 4
Question Number 119696 Answers: 2 Comments: 0
Question Number 119692 Answers: 3 Comments: 1
Question Number 119685 Answers: 0 Comments: 0
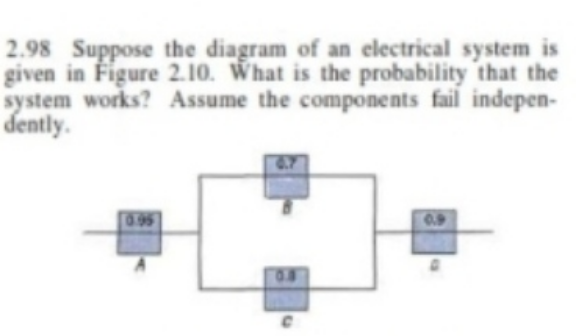
Question Number 119684 Answers: 1 Comments: 2

Question Number 119681 Answers: 4 Comments: 0
Question Number 119679 Answers: 1 Comments: 0
Question Number 119661 Answers: 0 Comments: 2
Question Number 119659 Answers: 2 Comments: 0
Question Number 119657 Answers: 1 Comments: 2
Question Number 119648 Answers: 1 Comments: 1
Question Number 119647 Answers: 1 Comments: 0

Question Number 119646 Answers: 0 Comments: 1

Question Number 119645 Answers: 1 Comments: 1
Question Number 119644 Answers: 5 Comments: 0
Question Number 119636 Answers: 1 Comments: 0
Question Number 119635 Answers: 1 Comments: 0
Question Number 119634 Answers: 2 Comments: 0
Question Number 119629 Answers: 1 Comments: 0
Pg 1000 Pg 1001 Pg 1002 Pg 1003 Pg 1004 Pg 1005 Pg 1006 Pg 1007 Pg 1008 Pg 1009
