Question and Answers Forum

AllQuestion and Answers: Page 1003

Question Number 119909 Answers: 2 Comments: 0

Given f(x)=((px+q)/(x+2)) , q≠ 0 f^(−1) (q) = −1 then f^(−1) (2q)=?

$${Given}\:{f}\left({x}\right)=\frac{{px}+{q}}{{x}+\mathrm{2}}\:,\:{q}\neq\:\mathrm{0} \\ $$$${f}^{−\mathrm{1}} \:\left({q}\right)\:=\:−\mathrm{1}\:{then}\:{f}^{−\mathrm{1}} \left(\mathrm{2}{q}\right)=? \\ $$

Question Number 119902 Answers: 3 Comments: 0

lim_(x→0) (cos x)^(1/(sin^2 x)) ?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}}} \:? \\ $$

Question Number 119896 Answers: 2 Comments: 1

Question Number 119894 Answers: 2 Comments: 0

Question Number 119893 Answers: 2 Comments: 0

Question Number 119892 Answers: 1 Comments: 0

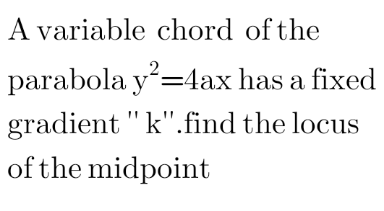
Question Number 119891 Answers: 0 Comments: 0

show that (d/dx) Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) lnt dt

$${show}\:{that}\: \\ $$$$\frac{{d}}{{dx}}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {lnt}\:{dt} \\ $$

Question Number 119876 Answers: 0 Comments: 0

Question Number 119875 Answers: 3 Comments: 1

Question Number 119866 Answers: 1 Comments: 4

Question Number 119867 Answers: 1 Comments: 2

lim_(x→∞) (((1+(1/(2n)))^n −(√e))/((1+(2/n))^n −e^2 ))=???

$${li}\underset{{x}\rightarrow\infty} {{m}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{{n}} −\sqrt{{e}}}{\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)^{{n}} −{e}^{\mathrm{2}} }=??? \\ $$

Question Number 119856 Answers: 0 Comments: 4

i have forgotten my password. how may i retrieve it? please help me or forward me to one of the developers please

$$\mathrm{i}\:\mathrm{have}\:\mathrm{forgotten}\:\mathrm{my}\:\mathrm{password}. \\ $$$$\mathrm{how}\:\mathrm{may}\:\mathrm{i}\:\mathrm{retrieve}\:\mathrm{it}? \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{or}\:\mathrm{forward}\:\mathrm{me}\:\mathrm{to} \\ $$$$\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{developers}\:\mathrm{please} \\ $$

Question Number 119852 Answers: 1 Comments: 0

lim_(n→∞) n^2 ∫ _0 ^(1/n) x^(x+1) dx =?

$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{\mathrm{2}} \:\int\:\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}}{{n}}} {\:}}{x}^{{x}+\mathrm{1}} \:{dx}\:=? \\ $$

Question Number 119849 Answers: 1 Comments: 0

Find all pair(x,y) of real numbers that are the solutions to the system { ((x^4 +2x^3 −y=−(1/4)+(√3))),((y^4 +2y^3 −x=−(1/4)−(√3))) :}

$${Find}\:{all}\:{pair}\left({x},{y}\right)\:{of}\:{real}\:{numbers} \\ $$$${that}\:{are}\:{the}\:{solutions}\:{to}\:{the}\:{system} \\ $$$$\begin{cases}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{y}=−\frac{\mathrm{1}}{\mathrm{4}}+\sqrt{\mathrm{3}}}\\{{y}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{3}} −{x}=−\frac{\mathrm{1}}{\mathrm{4}}−\sqrt{\mathrm{3}}}\end{cases} \\ $$

Question Number 119848 Answers: 1 Comments: 0

Solve in real numbers the equation (x)^(1/(3 )) + ((x−1))^(1/(3 )) + ((x+1))^(1/(3 )) = 0

$${Solve}\:{in}\:{real}\:{numbers}\:{the}\:{equation} \\ $$$$\sqrt[{\mathrm{3}\:}]{{x}}\:+\:\sqrt[{\mathrm{3}\:}]{{x}−\mathrm{1}}\:+\:\sqrt[{\mathrm{3}\:}]{{x}+\mathrm{1}}\:=\:\mathrm{0} \\ $$

Question Number 119839 Answers: 1 Comments: 0

Prove that sin x−cos^2 x+sin^3 x−cos^4 x+sin^5 x−cos^6 x +sin^7 x−cos^8 x+……=(√2)−1

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{sin}\:{x}−\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{3}} {x}−\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{5}} {x}−\mathrm{cos}^{\mathrm{6}} {x} \\ $$$$+\mathrm{sin}^{\mathrm{7}} {x}−\mathrm{cos}^{\mathrm{8}} {x}+\ldots\ldots=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$

Question Number 119837 Answers: 0 Comments: 0

find lim_(n→+∞) ∫_0 ^(√n) (1−(x/(√n)))^(√(2n)) arctan(((πx)/n))dx

$$\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{n}}} \left(\mathrm{1}−\frac{\mathrm{x}}{\sqrt{\mathrm{n}}}\right)^{\sqrt{\mathrm{2n}}} \:\mathrm{arctan}\left(\frac{\pi\mathrm{x}}{\mathrm{n}}\right)\mathrm{dx} \\ $$

Question Number 119835 Answers: 2 Comments: 1

If M and m are respectively the largest and the smallest integers that satisfying the inequality 6n^2 −5n≤99, find the value of M−m.

$$\mathrm{If}\:{M}\:\mathrm{and}\:{m}\:\mathrm{are}\:\mathrm{respectively}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{smallest}\:\mathrm{integers}\:\mathrm{that}\:\mathrm{satisfying}\:\mathrm{the} \\ $$$$\mathrm{inequality}\:\mathrm{6}{n}^{\mathrm{2}} −\mathrm{5}{n}\leqslant\mathrm{99},\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$${M}−{m}. \\ $$

Question Number 119832 Answers: 0 Comments: 0

evaluate: I = ∫_0 ^( 1) (((x+1)/x))^(x!) dx

$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{evaluate}:\:\:\:\:{I}\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{{x}}\right)^{{x}!} {dx} \\ $$$$ \\ $$$$ \\ $$

Question Number 119831 Answers: 0 Comments: 1

evaluate: I = ∫_1 ^( ∞) ((1/x))^x dx

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{evaluate}:\:\:\:{I}\:\:=\:\int_{\mathrm{1}} ^{\:\infty} \left(\frac{\mathrm{1}}{{x}}\right)^{{x}} {dx} \\ $$$$\: \\ $$$$\: \\ $$

Question Number 119812 Answers: 2 Comments: 0

Question Number 119808 Answers: 2 Comments: 0

f^(−1) (x)=3x^2 +2x f(8)=?

$${f}^{−\mathrm{1}} \left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x} \\ $$$${f}\left(\mathrm{8}\right)=? \\ $$

Question Number 119807 Answers: 1 Comments: 0

Let f be a real-valued function defined on the inte- rval [−1, 1]. If the area of the equilateral triangle with (0, 0) and (x, f(x)) as two vertices is (√3)/4, then f(x) is equal to (A) (√(1−x^2 )) (B) (√(1+x^2 )) (C) −(√(1−x^2 )) (D) −(√(1+x^2 ))

$$\mathrm{Let}\:{f}\:\mathrm{be}\:\mathrm{a}\:\mathrm{real}-\mathrm{valued}\:\mathrm{function}\:\mathrm{defined}\:\mathrm{on}\:\mathrm{the}\:\mathrm{inte}- \\ $$$$\mathrm{rval}\:\left[−\mathrm{1},\:\mathrm{1}\right].\:\mathrm{If}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{with} \\ $$$$\left(\mathrm{0},\:\mathrm{0}\right)\:\mathrm{and}\:\left(\mathrm{x},\:{f}\left(\mathrm{x}\right)\right)\:\mathrm{as}\:\mathrm{two}\:\mathrm{vertices}\:\mathrm{is}\:\sqrt{\mathrm{3}}/\mathrm{4},\:\mathrm{then}\:{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left(\mathrm{A}\right)\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{C}\right)\:−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$

Question Number 119803 Answers: 1 Comments: 0

Question Number 119802 Answers: 2 Comments: 0

Given a,b,c real number and not equal to 1. If log _a (b)+log _b (c)+log _c (a)=0 then (log _a (b))^3 +(log _b (c))^3 +(log _c (a))^3 =?

$${Given}\:{a},{b},{c}\:{real}\:{number}\:{and}\:{not}\:{equal}\:{to}\:\mathrm{1}. \\ $$$${If}\:\mathrm{log}\:_{{a}} \left({b}\right)+\mathrm{log}\:_{{b}} \left({c}\right)+\mathrm{log}\:_{{c}} \left({a}\right)=\mathrm{0}\:{then}\: \\ $$$$\left(\mathrm{log}\:_{{a}} \left({b}\right)\right)^{\mathrm{3}} +\left(\mathrm{log}\:_{{b}} \left({c}\right)\right)^{\mathrm{3}} +\left(\mathrm{log}\:_{{c}} \left({a}\right)\right)^{\mathrm{3}} =? \\ $$

Question Number 119800 Answers: 0 Comments: 2

Examples of functions such that f(x+y)=f(x)+f(y) for all x,y∈R

$$\mathrm{Examples}\:\mathrm{of}\:\mathrm{functions}\:\mathrm{such}\:\mathrm{that} \\ $$$${f}\left(\mathrm{x}+\mathrm{y}\right)={f}\left(\mathrm{x}\right)+{f}\left(\mathrm{y}\right)\:\mathrm{for}\:\mathrm{all}\:\mathrm{x},\mathrm{y}\in\mathbb{R} \\ $$

Pg 998 Pg 999 Pg 1000 Pg 1001 Pg 1002 Pg 1003 Pg 1004 Pg 1005 Pg 1006 Pg 1007

Contact: info@tinkutara.com