Question and Answers Forum

All Questions   Topic List

AllQuestion and Answers: Page 1000

Question Number 120186    Answers: 1   Comments: 0

Question Number 120185    Answers: 1   Comments: 0

solve for x, y∈Z (√x)+(√y)=(√(2020))

$${solve}\:{for}\:{x},\:{y}\in{Z} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{\mathrm{2020}} \\ $$

Question Number 120183    Answers: 0   Comments: 0

Question Number 123960    Answers: 0   Comments: 0

Question Number 120279    Answers: 0   Comments: 2

Question Number 120277    Answers: 2   Comments: 1

lim_(x→∞) x^3 {(√(x^2 +(√(x^4 +1)))) − x(√2) } ?

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} \:\left\{\sqrt{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}\:−\:{x}\sqrt{\mathrm{2}}\:\right\}\:? \\ $$

Question Number 120166    Answers: 1   Comments: 1

Question Number 120160    Answers: 1   Comments: 1

Question Number 120156    Answers: 1   Comments: 0

...♠ nice calculus♠... if cos^(−1) (x)+cos^(−1) (y)+cos^(−1) (z)=π✓ show that :: x^2 +y^2 +z^2 +2xyz=1 ✓ ... ♣M.N.july.1970♣...

$$\:\:\:\:\:\:\:\:...\spadesuit\:{nice}\:\:{calculus}\spadesuit... \\ $$$$\:\:{if}\:\:{cos}^{−\mathrm{1}} \left({x}\right)+{cos}^{−\mathrm{1}} \left({y}\right)+{cos}^{−\mathrm{1}} \left({z}\right)=\pi\checkmark \\ $$$$ \\ $$$$\:\:\:\:\:\:{show}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{xyz}=\mathrm{1}\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:...\:\clubsuit\mathscr{M}.\mathscr{N}.{july}.\mathrm{1970}\clubsuit... \\ $$

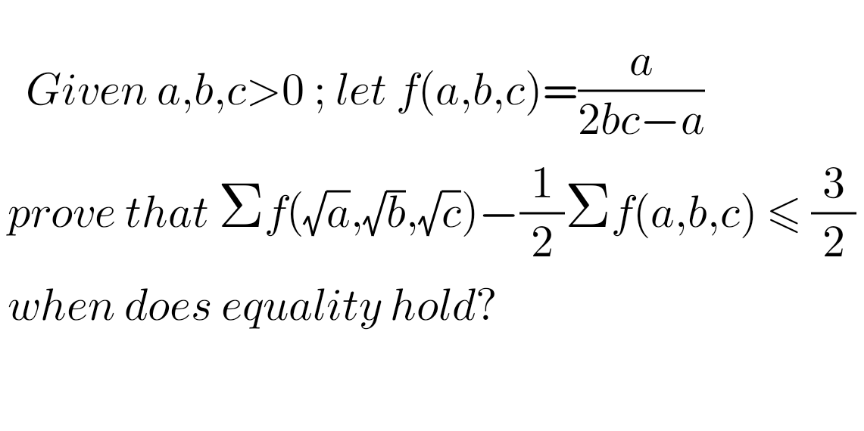
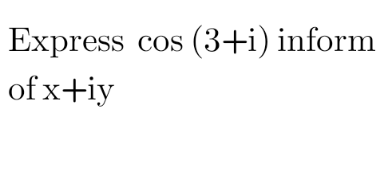
Question Number 120154    Answers: 1   Comments: 0

solve using LambertW function ((8/7))^x +17=25x

$${solve}\:{using}\:{LambertW}\:{function} \\ $$$$\left(\frac{\mathrm{8}}{\mathrm{7}}\right)^{{x}} +\mathrm{17}=\mathrm{25}{x} \\ $$

Question Number 120152    Answers: 0   Comments: 0

Determinate and construct the set of points M which have as affix z in each case: 1) arg(i−z)=0[π] 2) arg(z+1−i)=(π/6)[2π]

$$\mathrm{Determinate}\:\mathrm{and}\:\mathrm{construct}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{points}\:\mathrm{M} \\ $$$$\mathrm{which}\:\mathrm{have}\:\mathrm{as}\:\mathrm{affix}\:\mathrm{z}\:\:\mathrm{in}\:\mathrm{each}\:\mathrm{case}: \\ $$$$\left.\mathrm{1}\right)\:\mathrm{arg}\left(\mathrm{i}−\mathrm{z}\right)=\mathrm{0}\left[\pi\right] \\ $$$$\left.\mathrm{2}\right)\:\mathrm{arg}\left(\mathrm{z}+\mathrm{1}−\mathrm{i}\right)=\frac{\pi}{\mathrm{6}}\left[\mathrm{2}\pi\right] \\ $$$$ \\ $$

Question Number 120151    Answers: 0   Comments: 0

Represent in complex plane the set of points M which have as affix z such that ∣z∣=2 and arg(z+1)=(π/4)[π]

$$\mathrm{Represent}\:\mathrm{in}\:\mathrm{complex}\:\mathrm{plane}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{points} \\ $$$$\mathrm{M}\:\mathrm{which}\:\mathrm{have}\:\mathrm{as}\:\mathrm{affix}\:\mathrm{z}\:\mathrm{such}\:\mathrm{that}\:\mid\mathrm{z}\mid=\mathrm{2}\:\mathrm{and} \\ $$$$\mathrm{arg}\left(\mathrm{z}+\mathrm{1}\right)=\frac{\pi}{\mathrm{4}}\left[\pi\right] \\ $$

Question Number 120147    Answers: 1   Comments: 1

Question Number 120133    Answers: 0   Comments: 5

Question Number 120132    Answers: 0   Comments: 0

Suppose you are in a imagnary train which travels at the half of the speed of light. Suppose You have a brother who is 7 year smaller than you. He stands on the platform which you had left. After 1 hour of travelling on the train you come back on the platform. Then you observe something strange. You can see your brother looks older . So what is his age?(He was ten years old)

$${Suppose}\:{you}\:{are}\:{in}\:{a}\:{imagnary}\:{train}\:{which}\:{travels}\:{at}\:{the}\:{half}\: \\ $$$${of}\:{the}\:{speed}\:{of}\:{light}.\:{Suppose}\:{You}\:{have}\:{a}\:{brother}\:{who}\:{is}\:\mathrm{7}\:{year} \\ $$$${smaller}\:{than}\:{you}.\:{He}\:{stands}\:{on}\:{the}\:{platform}\:{which}\:{you}\:{had}\:{left}. \\ $$$${After}\:\mathrm{1}\:{hour}\:{of}\:{travelling}\:{on}\:{the}\:{train}\:{you}\:{come}\:{back}\:{on}\:{the} \\ $$$${platform}.\:{Then}\:{you}\:{observe}\:{something}\:{strange}.\:{You}\:{can}\:{see} \\ $$$${your}\:{brother}\:{looks}\:{older}\:.\:{So}\:{what}\:{is}\:{his}\:{age}?\left({He}\:{was}\:{ten}\:{years}\right. \\ $$$$\left.{old}\right) \\ $$

Question Number 120131    Answers: 1   Comments: 1

Question Number 120127    Answers: 2   Comments: 0

Question Number 120122    Answers: 0   Comments: 3

{ ((s_(12) =30)),((s_8 =4)) :} a_3 =?

$$\begin{cases}{{s}_{\mathrm{12}} =\mathrm{30}}\\{{s}_{\mathrm{8}} =\mathrm{4}}\end{cases}\:\:\:{a}_{\mathrm{3}} =? \\ $$

Question Number 120120    Answers: 2   Comments: 0

{ ((log _a (x) = 8)),((log _b (x) = 3 )),((log _c (x) = 6)) :} ⇒ log _(abc) (x)=?

$$\begin{cases}{\mathrm{log}\:_{{a}} \left({x}\right)\:=\:\mathrm{8}}\\{\mathrm{log}\:_{{b}} \left({x}\right)\:=\:\mathrm{3}\:}\\{\mathrm{log}\:_{{c}} \left({x}\right)\:=\:\mathrm{6}}\end{cases}\:\Rightarrow\:\mathrm{log}\:_{{abc}} \:\left({x}\right)=? \\ $$

Question Number 120118    Answers: 0   Comments: 2

Question Number 120140    Answers: 2   Comments: 0

Question Number 120110    Answers: 2   Comments: 0

{ ((((4x^2 )/(4x^2 +1)) = y)),((((4y^2 )/(4y^2 +1)) = z )),((((4z^2 )/(4z^2 +1)) = x)) :} where x,y,z ≠ 0

$$\begin{cases}{\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}\:=\:{y}}\\{\frac{\mathrm{4}{y}^{\mathrm{2}} }{\mathrm{4}{y}^{\mathrm{2}} +\mathrm{1}}\:=\:{z}\:}\\{\frac{\mathrm{4}{z}^{\mathrm{2}} }{\mathrm{4}{z}^{\mathrm{2}} +\mathrm{1}}\:=\:{x}}\end{cases} \\ $$$${where}\:{x},{y},{z}\:\neq\:\mathrm{0}\: \\ $$

Question Number 120109    Answers: 0   Comments: 0

Question Number 120108    Answers: 0   Comments: 0

(x^4 +ax^2 +a^2 )^2 +x^6 =1 solve for: x,a∈R

$$\left(\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\boldsymbol{\mathrm{ax}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{\mathrm{6}} =\mathrm{1} \\ $$$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}:\:\:\mathrm{x},\mathrm{a}\in\boldsymbol{\mathrm{R}} \\ $$

Question Number 120102    Answers: 2   Comments: 0

Θ = ∫ ((4x^(−1) +8x^(−3) )/(x^2 (√(x^4 +2x^2 +2)))) dx

$$\:\Theta\:=\:\int\:\frac{\mathrm{4}{x}^{−\mathrm{1}} +\mathrm{8}{x}^{−\mathrm{3}} }{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}}}\:{dx}\: \\ $$

Question Number 120092    Answers: 3   Comments: 1

  Pg 995      Pg 996      Pg 997      Pg 998      Pg 999      Pg 1000      Pg 1001      Pg 1002      Pg 1003      Pg 1004   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com