
AlgebraQuestion and Answers: Page 93
Question Number 181099 Answers: 2 Comments: 0
Question Number 181089 Answers: 1 Comments: 0

Question Number 181079 Answers: 6 Comments: 2
Question Number 181041 Answers: 0 Comments: 0
Question Number 181020 Answers: 1 Comments: 0
Question Number 181007 Answers: 1 Comments: 0
Question Number 180977 Answers: 3 Comments: 0
Question Number 180953 Answers: 2 Comments: 0
Question Number 181066 Answers: 1 Comments: 1
Question Number 180943 Answers: 2 Comments: 0
Question Number 180938 Answers: 2 Comments: 0
Question Number 180923 Answers: 1 Comments: 0

Question Number 180889 Answers: 0 Comments: 1
Question Number 180873 Answers: 1 Comments: 2
Question Number 180896 Answers: 0 Comments: 1
Question Number 180856 Answers: 1 Comments: 0
Question Number 180894 Answers: 3 Comments: 2
$${x}^{\mathrm{3}} +{x}=\mathrm{1} \\ $$$${x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} =? \\ $$
Question Number 180800 Answers: 0 Comments: 0
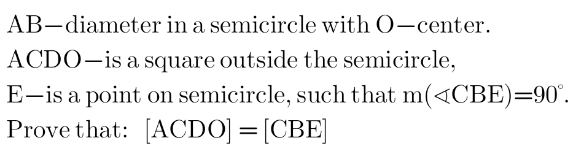
Question Number 180785 Answers: 2 Comments: 0
Question Number 180778 Answers: 0 Comments: 0
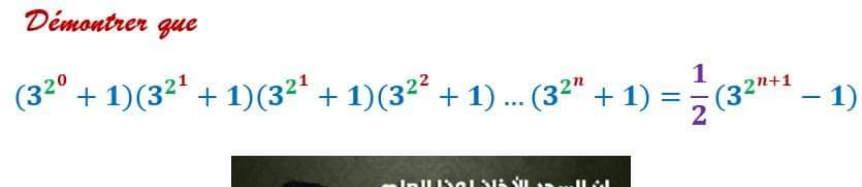
Question Number 180759 Answers: 1 Comments: 0
Question Number 180728 Answers: 1 Comments: 0
Question Number 180744 Answers: 2 Comments: 2

Question Number 180604 Answers: 1 Comments: 0
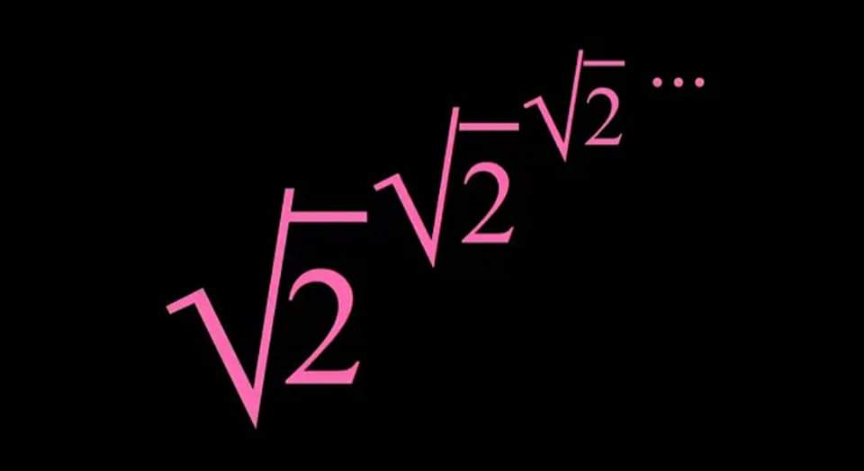
Question Number 180603 Answers: 0 Comments: 1
Question Number 180569 Answers: 1 Comments: 1
