Question and Answers Forum

AlgebraQuestion and Answers: Page 91

Question Number 185693 Answers: 1 Comments: 1

If k > 0 and f(x) = (x/(∣x∣)) Find f(- (2/7) k) + f( - 2k) = ?

$$\mathrm{If}\:\:\:\mathrm{k}\:>\:\mathrm{0}\:\:\:\mathrm{and}\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mid\mathrm{x}\mid} \\ $$$$\mathrm{Find}\:\:\:\mathrm{f}\left(-\:\frac{\mathrm{2}}{\mathrm{7}}\:\mathrm{k}\right)\:+\:\mathrm{f}\left(\:-\:\mathrm{2k}\right)\:=\:? \\ $$

Question Number 185692 Answers: 0 Comments: 0

Given u^→ =(−2,3,1) and v^→ =(7,1,−4) verify cauchy−schwartz inequarity and triangle inequarty

$${Given}\: \\ $$$$\overset{\rightarrow} {{u}}=\left(−\mathrm{2},\mathrm{3},\mathrm{1}\right)\:\:{and}\:\overset{\rightarrow} {{v}}=\left(\mathrm{7},\mathrm{1},−\mathrm{4}\right) \\ $$$${verify}\:{cauchy}−{schwartz}\: \\ $$$${inequarity}\:{and}\:{triangle}\:{inequarty} \\ $$

Question Number 185684 Answers: 0 Comments: 7

17 , 78, 143, 353, ? a)366 b)0 c)398 d)435

$$\mathrm{17}\:,\:\mathrm{78},\:\mathrm{143},\:\mathrm{353},\:? \\ $$$$\left.\mathrm{a}\left.\right)\left.\mathrm{3}\left.\mathrm{66}\:\:\:\:\:\mathrm{b}\right)\mathrm{0}\:\:\:\:\:\mathrm{c}\right)\mathrm{398}\:\:\:\:\:\mathrm{d}\right)\mathrm{435} \\ $$

Question Number 185673 Answers: 1 Comments: 0

Question Number 185668 Answers: 2 Comments: 0

Find: (1/(sin 10°)) − 4 sin 70° = ?

$$\mathrm{Find}:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{10}°}\:−\:\mathrm{4}\:\mathrm{sin}\:\mathrm{70}°\:=\:? \\ $$

Question Number 185665 Answers: 1 Comments: 0

f(((2x−1)/(3x+2)))=((x−1)/(x−2)) faind f^(−1) (2)=?

$${f}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{3}{x}+\mathrm{2}}\right)=\frac{{x}−\mathrm{1}}{{x}−\mathrm{2}}\:\:\:\:\:\:{faind}\:\:\:{f}^{−\mathrm{1}} \left(\mathrm{2}\right)=? \\ $$

Question Number 185663 Answers: 0 Comments: 0

Question Number 185599 Answers: 4 Comments: 3

x!=x^3 −x faind x=?

$${x}!={x}^{\mathrm{3}} −{x}\:\:\:\:\:\:\:\:\:\:{faind}\:{x}=? \\ $$

Question Number 185598 Answers: 0 Comments: 0

Question Number 185624 Answers: 1 Comments: 0

Question Number 185580 Answers: 1 Comments: 0

Question Number 185542 Answers: 2 Comments: 0

Question Number 185536 Answers: 1 Comments: 1

x^4 +x^(ln5) =19 x^(lnx) +ln^2 x=4 x=?

$${x}^{\mathrm{4}} +{x}^{{ln}\mathrm{5}} =\mathrm{19} \\ $$$${x}^{{lnx}} +{ln}^{\mathrm{2}} {x}=\mathrm{4} \\ $$$${x}=? \\ $$

Question Number 185529 Answers: 2 Comments: 0

Question Number 185522 Answers: 0 Comments: 1

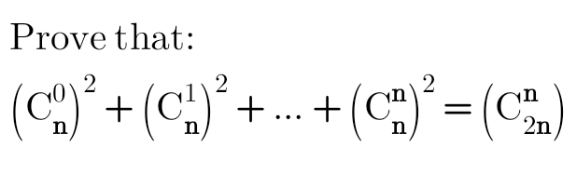
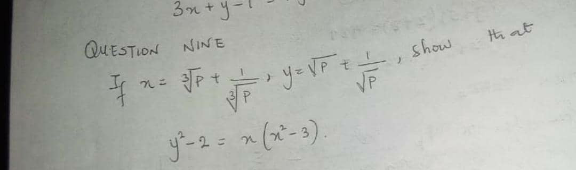
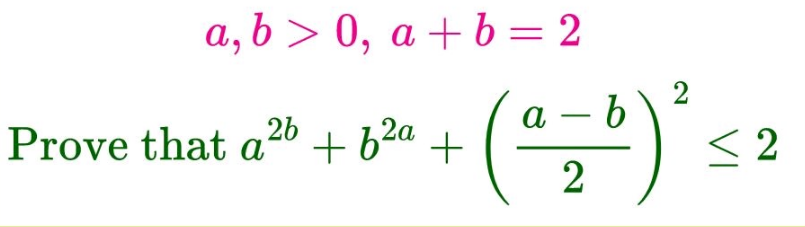
Question Number 185515 Answers: 1 Comments: 0

At a party with “m” people, a lady dances with p gentlemen, the second with p + 1, the third one with p + 2, and so on until the last one dances with all the gentlemen, find the number of ladies who attended the party in terms of “m”and “p”.

$$\:{At}\:{a}\:{party}\:{with}\:``{m}''\:{people},\:{a}\:{lady}\:{dances} \\ $$$$\:{with}\:{p}\:{gentlemen},\:{the}\:{second}\:{with}\:{p}\:+\:\mathrm{1},\: \\ $$$$\:{the}\:{third}\:{one}\:{with}\:{p}\:+\:\mathrm{2},\:{and}\:{so}\:{on}\:{until}\:{the} \\ $$$$\:{last}\:{one}\:{dances}\:{with}\:{all}\:{the}\:{gentlemen},\: \\ $$$$\:{find}\:{the}\:{number}\:{of}\:{ladies}\:{who}\:{attended}\:{the} \\ $$$$\:{party}\:{in}\:{terms}\:{of}\:``{m}''{and}\:``{p}''. \\ $$

Question Number 185481 Answers: 0 Comments: 0