Question and Answers Forum

AlgebraQuestion and Answers: Page 65

Question Number 194238 Answers: 1 Comments: 0

Question Number 194226 Answers: 3 Comments: 0

If x^2 − 65x = 64(√x) then (√(x − (√x) )) = ?

$$ \\ $$$$\mathrm{If}\:{x}^{\mathrm{2}} \:−\:\mathrm{65}{x}\:=\:\mathrm{64}\sqrt{{x}}\:\mathrm{then}\:\sqrt{{x}\:−\:\sqrt{{x}}\:}\:=\:? \\ $$

Question Number 194219 Answers: 1 Comments: 0

Question Number 194218 Answers: 1 Comments: 2

Question Number 194216 Answers: 1 Comments: 0

Question Number 194209 Answers: 0 Comments: 0

((1+kx))^(1/3) +x = 1 has two real roots . ⇒ k=? kx+1= 1−3x+3x^2 −x^( 3) x^( 3) −3x^( 2) + (k+3)x=0 x=0 x^( 2) −3x +k+3=0 1: Δ=0 9 − 4k −12=0 k= ((−3)/4) 2: k=−3 ⇒ x=0 is a root of x^( 2) −3x+k+3=0 ∴ k= ((−3)/4) or k=−3

$$ \\ $$$$\:\:\:\:\:\:\sqrt[{\mathrm{3}}]{\mathrm{1}+{kx}}\:+{x}\:=\:\mathrm{1}\:\:\:{has} \\ $$$$\:\:\:\:\:\:{two}\:{real}\:{roots}\:.\:\:\Rightarrow\:{k}=? \\ $$$$\:\:\:{kx}+\mathrm{1}=\:\mathrm{1}−\mathrm{3}{x}+\mathrm{3}{x}^{\mathrm{2}} −{x}^{\:\mathrm{3}} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:{x}^{\:\mathrm{3}} \:−\mathrm{3}{x}^{\:\mathrm{2}} +\:\left({k}+\mathrm{3}\right){x}=\mathrm{0} \\ $$$$\:\:\:\:\:{x}=\mathrm{0} \\ $$$$\:\:\:\:\:{x}^{\:\mathrm{2}} −\mathrm{3}{x}\:+{k}+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{1}:\:\:\Delta=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{9}\:−\:\mathrm{4}{k}\:−\mathrm{12}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{k}=\:\frac{−\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\mathrm{2}:\:\:{k}=−\mathrm{3}\:\Rightarrow\:{x}=\mathrm{0}\:{is}\:{a}\:{root}\:{of} \\ $$$$\:\:\:\:\:\:{x}^{\:\mathrm{2}} −\mathrm{3}{x}+{k}+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\therefore\:\:\:\:\:\:{k}=\:\frac{−\mathrm{3}}{\mathrm{4}}\:\:\:\:{or}\:\:\:{k}=−\mathrm{3} \\ $$

Question Number 194207 Answers: 0 Comments: 0

Solve for x x^(x−4) =(√(3 ))

$$\:\:\:\:\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\: \\ $$$$\:\:\:\:\mathrm{x}^{\mathrm{x}−\mathrm{4}} \:\:=\sqrt{\mathrm{3}\:} \\ $$

Question Number 194206 Answers: 1 Comments: 0

Question Number 194204 Answers: 1 Comments: 0

Question Number 194197 Answers: 1 Comments: 0

Question Number 194191 Answers: 1 Comments: 0

Question Number 194170 Answers: 0 Comments: 0

Question Number 194169 Answers: 0 Comments: 0

Question Number 194166 Answers: 1 Comments: 0

Question Number 194163 Answers: 0 Comments: 0

Let a , b , c be positive real numbers prove that (a/b)+(b/c)+(c/a)+((3^3 (√(abc)))/(a+b+c))≥4

$$\boldsymbol{{Let}}\:\boldsymbol{{a}}\:,\:\boldsymbol{{b}}\:,\:\boldsymbol{{c}}\:\:\:\boldsymbol{{be}}\:\boldsymbol{{positive}}\:\boldsymbol{{real}}\:\boldsymbol{{numbers}} \\ $$$$\boldsymbol{{prove}}\:\boldsymbol{{that}} \\ $$$$\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}}+\frac{\boldsymbol{{b}}}{\boldsymbol{{c}}}+\frac{\boldsymbol{{c}}}{\boldsymbol{{a}}}+\frac{\mathrm{3}^{\mathrm{3}} \sqrt{{abc}}}{\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}}\geqslant\mathrm{4} \\ $$

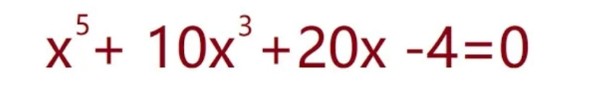
Question Number 194159 Answers: 0 Comments: 0

...anybody tried question 193484? It′s not as hard as it may seem.

$$...\mathrm{anybody}\:\mathrm{tried}\:\mathrm{question}\:\mathrm{193484}? \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{as}\:\mathrm{hard}\:\mathrm{as}\:\mathrm{it}\:\mathrm{may}\:\mathrm{seem}. \\ $$

Question Number 194140 Answers: 1 Comments: 0

prove it : ((n),(k) )^( 2) ≥ ((( n)),((k−1)) ) × ((( n)),((k+1)) ) ; 1≤k≤n−1

$${prove}\:{it}\:: \\ $$$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\:\mathrm{2}} \geqslant\:\begin{pmatrix}{\:\:\:\:{n}}\\{{k}−\mathrm{1}}\end{pmatrix}\:×\begin{pmatrix}{\:\:{n}}\\{{k}+\mathrm{1}}\end{pmatrix}\:\:\:\:\:;\:\:\:\mathrm{1}\leqslant{k}\leqslant{n}−\mathrm{1} \\ $$$$ \\ $$

Question Number 194135 Answers: 3 Comments: 0

determinant (((((23!−23)/(1.1!+2.2!+3.3!+...+21.21!)) =?)))

$$\:\:\:\:\:\:\begin{array}{|c|}{\frac{\mathrm{23}!−\mathrm{23}}{\mathrm{1}.\mathrm{1}!+\mathrm{2}.\mathrm{2}!+\mathrm{3}.\mathrm{3}!+...+\mathrm{21}.\mathrm{21}!}\:=?}\\\hline\end{array} \\ $$

Question Number 194113 Answers: 1 Comments: 0

Question Number 194105 Answers: 1 Comments: 0

x , y , z are positive real numbers if x^4 +y^4 +z^4 =1 Then find the minimum value of (x^3 /(1−x^8 ))+(y^3 /(1−y^8 ))+(z^3 /(1−z^8 ))

$$ \\ $$$${x}\:,\:{y}\:,\:{z}\:{are}\:{positive}\:{real}\:{numbers}\:{if}\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{1} \\ $$$${Then}\:{find}\:{the}\:{minimum}\:{value}\:{of}\: \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{8}} }+\frac{{y}^{\mathrm{3}} }{\mathrm{1}−{y}^{\mathrm{8}} }+\frac{{z}^{\mathrm{3}} }{\mathrm{1}−{z}^{\mathrm{8}} } \\ $$

Question Number 194086 Answers: 1 Comments: 1

f(x)=2y^2 +4y+3 then a_(0 ) equle to a) p(5) b) 7 c) 3 d) not defined

$${f}\left({x}\right)=\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{3}\:\:{then}\:{a}_{\mathrm{0}\:} {equle}\:{to} \\ $$$$\left.{a}\left.\right)\:\:\:{p}\left(\mathrm{5}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}\right)\:\:\:\:\mathrm{7} \\ $$$$\left.{c}\left.\right)\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}\right)\:{not}\:{defined} \\ $$

Question Number 194065 Answers: 0 Comments: 0

Question Number 194057 Answers: 0 Comments: 0

find all functions such that f(x)f(y) = x^a f((y/2))+y^b f((x/2))

$${find}\:{all}\:{functions}\:{such}\:{that} \\ $$$${f}\left({x}\right){f}\left({y}\right)\:=\:{x}^{{a}} {f}\left(\frac{{y}}{\mathrm{2}}\right)+{y}^{{b}} {f}\left(\frac{{x}}{\mathrm{2}}\right) \\ $$

Question Number 194037 Answers: 3 Comments: 0

Let a_1 ,a_2 ....a_n ∈R^+ , a_1 +a_2 +.....a_n =1 prove that: (a_1 /(2−a_1 ))+(a_2 /(2−a_2 )).......(a_n /(2−a_n ))≥(n/(2n−1))

$$ \\ $$$${Let}\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ....{a}_{{n}} \in{R}^{+} ,\:{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +.....{a}_{{n}} =\mathrm{1} \\ $$$${prove}\:{that}: \\ $$$$\frac{{a}_{\mathrm{1}} }{\mathrm{2}−{a}_{\mathrm{1}} }+\frac{{a}_{\mathrm{2}} }{\mathrm{2}−{a}_{\mathrm{2}} }.......\frac{{a}_{{n}} }{\mathrm{2}−{a}_{{n}} }\geqslant\frac{{n}}{\mathrm{2}{n}−\mathrm{1}} \\ $$

Question Number 193978 Answers: 1 Comments: 0

Question Number 193972 Answers: 0 Comments: 4

Pg 60 Pg 61 Pg 62 Pg 63 Pg 64 Pg 65 Pg 66 Pg 67 Pg 68 Pg 69

Contact: info@tinkutara.com