Question and Answers Forum

AlgebraQuestion and Answers: Page 64

Question Number 197623 Answers: 1 Comments: 1

x,y∈N 162 ∙ x^2 = y^3 min(x+y)=?

$$\mathrm{x},\mathrm{y}\in\mathbb{N} \\ $$$$\mathrm{162}\:\centerdot\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{y}^{\mathrm{3}} \\ $$$$\mathrm{min}\left(\mathrm{x}+\mathrm{y}\right)=? \\ $$

Question Number 197618 Answers: 1 Comments: 0

Question Number 197609 Answers: 2 Comments: 0

((x+3)/(2022)) + ((x+2)/(2023)) + ((x+1)/(2024)) + (x/(2025)) = −4

$$\:\:\:\frac{{x}+\mathrm{3}}{\mathrm{2022}}\:+\:\frac{{x}+\mathrm{2}}{\mathrm{2023}}\:+\:\frac{{x}+\mathrm{1}}{\mathrm{2024}}\:+\:\frac{{x}}{\mathrm{2025}}\:=\:−\mathrm{4} \\ $$

Question Number 197567 Answers: 1 Comments: 0

Question Number 197530 Answers: 2 Comments: 0

f(x)−(x^2 /2)f′′(x)=0 f(x)=?

$$\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{f}''\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=? \\ $$

Question Number 197476 Answers: 1 Comments: 7

find the sum (1/(x+1))+(2/(x^2 +1))+(4/(x^4 +1))+.........+(2^n /(x^2^n +1)) = ??

$$ \\ $$$$\:\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\:\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} +\mathrm{1}}+.........+\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}}\:\:=\:?? \\ $$

Question Number 197464 Answers: 1 Comments: 0

Question Number 197455 Answers: 1 Comments: 0

f(x)=((2x+6)/2)+6−x g(x)=(√(x^(99) +x^(98) +x^(97) +.....+x)) f(g(1))+f(g(2))+.........+f(g(100))=?

$${f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{6}}{\mathrm{2}}+\mathrm{6}−{x} \\ $$$${g}\left({x}\right)=\sqrt{{x}^{\mathrm{99}} +{x}^{\mathrm{98}} +{x}^{\mathrm{97}} +.....+{x}} \\ $$$${f}\left({g}\left(\mathrm{1}\right)\right)+{f}\left({g}\left(\mathrm{2}\right)\right)+.........+{f}\left({g}\left(\mathrm{100}\right)\right)=? \\ $$

Question Number 197422 Answers: 2 Comments: 0

Question Number 197419 Answers: 1 Comments: 0

Question Number 197409 Answers: 1 Comments: 4

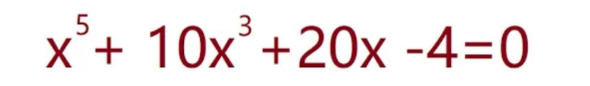
Question Number 197393 Answers: 1 Comments: 0

Question Number 197360 Answers: 1 Comments: 0

Find: ∫_0 ^( ∞) sin^2 ( (√x) ) e^(−x) dx = ?

$$\mathrm{Find}: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{sin}^{\mathrm{2}} \:\left(\:\sqrt{\mathrm{x}}\:\right)\:\mathrm{e}^{−\boldsymbol{\mathrm{x}}} \:\mathrm{dx}\:=\:? \\ $$

Question Number 197312 Answers: 1 Comments: 0

(((log_2 20)^2 −(log_2 5)^2 )/(log_2 10))=?

$$\frac{\left({log}_{\mathrm{2}} \mathrm{20}\right)^{\mathrm{2}} −\left({log}_{\mathrm{2}} \mathrm{5}\right)^{\mathrm{2}} }{{log}_{\mathrm{2}} \mathrm{10}}=? \\ $$

Question Number 197275 Answers: 1 Comments: 0

how do i prove this, help please. ∣((x^2 −2x−3)/(x^2 +2x+4))∣≤(5/4),∣x∣≤2

$$ \\ $$$$\:{how}\:{do}\:{i}\:{prove}\:{this},\:{help}\:{please}. \\ $$$$\:\mid\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\mid\leqslant\frac{\mathrm{5}}{\mathrm{4}},\mid{x}\mid\leqslant\mathrm{2} \\ $$$$ \\ $$$$ \\ $$

Question Number 197248 Answers: 0 Comments: 3

a,b,c∈R ((a + 2b − 3ac)/(3ac)) = ((a + 4b − bc)/b) Find: ((2b)/a) − ((3a)/b)

$$\mathrm{a},\mathrm{b},\mathrm{c}\in\mathbb{R} \\ $$$$\frac{\mathrm{a}\:+\:\mathrm{2b}\:−\:\mathrm{3ac}}{\mathrm{3ac}}\:\:=\:\:\frac{\mathrm{a}\:+\:\mathrm{4b}\:−\:\mathrm{bc}}{\mathrm{b}} \\ $$$$\mathrm{Find}:\:\:\:\frac{\mathrm{2b}}{\mathrm{a}}\:−\:\frac{\mathrm{3a}}{\mathrm{b}} \\ $$

Question Number 197171 Answers: 1 Comments: 0

2^(log_3 (x^2 +1)) +2×(x^2 +1)^(log_3 2) =12 ⇒x=?

$$\mathrm{2}^{{log}_{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)} +\mathrm{2}×\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{log}_{\mathrm{3}} \mathrm{2}} \:=\mathrm{12} \\ $$$$\Rightarrow{x}=? \\ $$$$ \\ $$

Question Number 197125 Answers: 1 Comments: 1

Question Number 197064 Answers: 2 Comments: 0

Question Number 197034 Answers: 1 Comments: 0

Question Number 197003 Answers: 0 Comments: 0

Question Number 197002 Answers: 0 Comments: 1

Question Number 196964 Answers: 2 Comments: 0

Question Number 196893 Answers: 1 Comments: 0

Question Number 196885 Answers: 2 Comments: 0

Question Number 196872 Answers: 1 Comments: 0

Let ξ be a positive Root of x^2 −2023x−1 Define a sequence ϕ_i such That ϕ_0 =1 ϕ_(n+1) =⌊ϕ_n ξ⌋, find The Remainder When ϕ_(2023 ) is divided by (√ϕ_2 )

$${Let}\:\xi\:{be}\:{a}\:{positive}\:{Root}\:{of}\:{x}^{\mathrm{2}} −\mathrm{2023}{x}−\mathrm{1} \\ $$$${Define}\:{a}\:{sequence}\:\varphi_{{i}} \:{such}\:{That}\:\varphi_{\mathrm{0}} =\mathrm{1} \\ $$$$\varphi_{{n}+\mathrm{1}} =\lfloor\varphi_{{n}} \xi\rfloor,\:{find}\:{The}\:{Remainder}\:{When}\:\varphi_{\mathrm{2023}\:} {is}\:{divided}\:{by}\:\sqrt{\varphi_{\mathrm{2}} } \\ $$

Pg 59 Pg 60 Pg 61 Pg 62 Pg 63 Pg 64 Pg 65 Pg 66 Pg 67 Pg 68

Contact: info@tinkutara.com