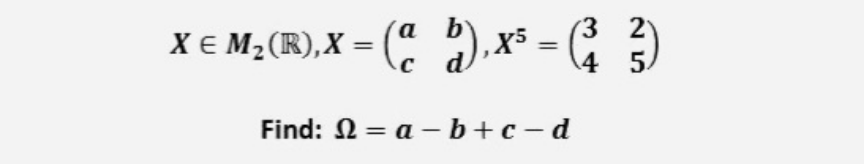Question and Answers Forum

All Questions   Topic List

AlgebraQuestion and Answers: Page 46

Question Number 206082    Answers: 2   Comments: 0

If cos𝛂 = sin𝛂 + (1/( (√3))) Find sin2𝛂 = ?

$$\mathrm{If}\:\:\:\mathrm{cos}\boldsymbol{\alpha}\:=\:\mathrm{sin}\boldsymbol{\alpha}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Find}\:\:\:\mathrm{sin2}\boldsymbol{\alpha}\:=\:? \\ $$

Question Number 206074    Answers: 0   Comments: 1

(x_1 βˆ’ x_2 + x_3 )^2 = x_2 (x_4 + x_5 βˆ’ x_2 ) (x_2 βˆ’ x_3 + x_4 )^2 = x_3 (x_5 + x_1 βˆ’ x_3 ) (x_3 βˆ’ x_4 + x_5 )^2 = x_4 (x_1 + x_2 βˆ’ x_4 ) (x_4 βˆ’ x_5 + x_1 )^2 = x_5 (x_2 + x_3 βˆ’ x_5 ) (x_5 βˆ’ x_1 + x_2 )^2 = x_1 (x_3 + x_4 βˆ’ x_1 ) Find ((2x_1 + x_2 + x_3 )/(3x_4 βˆ’ x_5 )) .

$$\left({x}_{\mathrm{1}} \:βˆ’\:{x}_{\mathrm{2}} \:+\:{x}_{\mathrm{3}} \right)^{\mathrm{2}} \:=\:{x}_{\mathrm{2}} \left({x}_{\mathrm{4}} \:+\:{x}_{\mathrm{5}} \:βˆ’\:{x}_{\mathrm{2}} \right) \\ $$$$\left({x}_{\mathrm{2}} \:βˆ’\:{x}_{\mathrm{3}} \:+\:{x}_{\mathrm{4}} \right)^{\mathrm{2}} \:=\:{x}_{\mathrm{3}} \left({x}_{\mathrm{5}} \:+\:{x}_{\mathrm{1}} \:βˆ’\:{x}_{\mathrm{3}} \right) \\ $$$$\left({x}_{\mathrm{3}} \:βˆ’\:{x}_{\mathrm{4}} \:+\:{x}_{\mathrm{5}} \right)^{\mathrm{2}} \:=\:{x}_{\mathrm{4}} \left({x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \:βˆ’\:{x}_{\mathrm{4}} \right) \\ $$$$\left({x}_{\mathrm{4}} \:βˆ’\:{x}_{\mathrm{5}} \:+\:{x}_{\mathrm{1}} \right)^{\mathrm{2}} \:=\:{x}_{\mathrm{5}} \left({x}_{\mathrm{2}} \:+\:{x}_{\mathrm{3}} \:βˆ’\:{x}_{\mathrm{5}} \right) \\ $$$$\left({x}_{\mathrm{5}} \:βˆ’\:{x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \right)^{\mathrm{2}} \:=\:{x}_{\mathrm{1}} \left({x}_{\mathrm{3}} \:+\:{x}_{\mathrm{4}} \:βˆ’\:{x}_{\mathrm{1}} \right) \\ $$$$\mathrm{Find}\:\frac{\mathrm{2}{x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \:+\:{x}_{\mathrm{3}} }{\mathrm{3}{x}_{\mathrm{4}} \:βˆ’\:{x}_{\mathrm{5}} }\:. \\ $$

Question Number 206066    Answers: 2   Comments: 0

Find: (3/4) βˆ™ (8/9) βˆ™ ((15)/(16)) βˆ™ ... βˆ™ ((120)/(121)) = ?

$$\mathrm{Find}: \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\:\centerdot\:\frac{\mathrm{8}}{\mathrm{9}}\:\centerdot\:\frac{\mathrm{15}}{\mathrm{16}}\:\centerdot\:...\:\centerdot\:\frac{\mathrm{120}}{\mathrm{121}}\:=\:? \\ $$

Question Number 206063    Answers: 2   Comments: 0

If (x + (√(1 + x^2 )))(y + (√(1 + y^2 ))) = 1 then find (x + y)^2 .

$$\mathrm{If}\:\left({x}\:+\:\sqrt{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\right)\left({y}\:+\:\sqrt{\mathrm{1}\:+\:{y}^{\mathrm{2}} }\right)\:=\:\mathrm{1}\:\mathrm{then} \\ $$$$\mathrm{find}\:\left({x}\:+\:{y}\right)^{\mathrm{2}} . \\ $$

Question Number 206025    Answers: 2   Comments: 0

2^(2024) = x (mod 10)

$$\:\:\:\:\:\mathrm{2}^{\mathrm{2024}} \:=\:{x}\:\left({mod}\:\mathrm{10}\right)\: \\ $$

Question Number 205990    Answers: 2   Comments: 0

If x = ((√3)/2) then (((√(1 + x)) + (√(1 βˆ’ x)))/( (√(1 + x)) βˆ’ (√(1 βˆ’ x)))) = ?

$$\mathrm{If}\:{x}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{then}\:\frac{\sqrt{\mathrm{1}\:+\:{x}}\:+\:\sqrt{\mathrm{1}\:βˆ’\:{x}}}{\:\sqrt{\mathrm{1}\:+\:{x}}\:βˆ’\:\sqrt{\mathrm{1}\:βˆ’\:{x}}}\:=\:? \\ $$

Question Number 205988    Answers: 1   Comments: 0

Given f(x+1)=2^(f(x)) .f(1) and f(1)= 16 then f(2016)=?

$$\:\:{Given}\:{f}\left({x}+\mathrm{1}\right)=\mathrm{2}^{{f}\left({x}\right)} .{f}\left(\mathrm{1}\right) \\ $$$$\:\:{and}\:{f}\left(\mathrm{1}\right)=\:\mathrm{16}\: \\ $$$$\:\:{then}\:{f}\left(\mathrm{2016}\right)=? \\ $$

Question Number 205941    Answers: 1   Comments: 0

2+(2/(2βˆ’(2/(2+(2/(2βˆ’(2/(2+(2/3))))))))) =?

$$\:\:\:\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}βˆ’\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}βˆ’\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{3}}}}}}\:=?\: \\ $$$$\: \\ $$

Question Number 205971    Answers: 2   Comments: 1

9 Mathematical Analysis ( I ) (X , d ) is a metric space and { p_n }_(n=1) ^∞ is a sequence in X such that , p_n β†’^(convergent) p . If , K= {p_n }_(n=1) ^∞ βˆͺ { p } then prove K , is compact in X .

$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{9}\:\:\mathscr{M}{athematical}\:\:\:\:\mathscr{A}{nalysis}\:\left(\:{I}\:\right) \\ $$$$\:\:\left({X}\:,\:{d}\:\right)\:{is}\:{a}\:{metric}\:{space}\:{and}\:\:\:\:\:\:\: \\ $$$$\:\:\:\left\{\:{p}_{{n}} \right\}_{{n}=\mathrm{1}} ^{\infty} {is}\:{a}\:{sequence}\:{in}\:{X}\: \\ $$$$\:\:\:\:\:{such}\:{that}\:,\:{p}_{{n}} \overset{{convergent}} {\rightarrow}\:{p}\:.\:{If}\:,\:{K}=\:\left\{{p}_{{n}} \right\}_{{n}=\mathrm{1}} ^{\infty} \cup\:\left\{\:{p}\:\right\}\:{then} \\ $$$$\:\:\:\:\:{prove}\:\:{K}\:,\:{is}\:{compact}\:{in}\:{X}\:.\: \\ $$$$\:\:\:\: \\ $$

Question Number 205914    Answers: 4   Comments: 2

if a+b+c+d+e+f=10 and a^2 +b^2 +c^2 +d^2 +e^2 +f^2 =25, find a_(min) and f_(max) .

$${if}\:{a}+{b}+{c}+{d}+{e}+{f}=\mathrm{10}\:{and} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +{e}^{\mathrm{2}} +{f}^{\mathrm{2}} =\mathrm{25},\:{find} \\ $$$${a}_{{min}} \:{and}\:{f}_{{max}} . \\ $$

Question Number 205885    Answers: 2   Comments: 0

Find: lim_(nβ†’βˆž) ()^(1/n) (((2n)),(( n)) ) = ?

$$\mathrm{Find}:\:\:\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\boldsymbol{\mathrm{n}}}]{}\begin{pmatrix}{\mathrm{2n}}\\{\:\:\mathrm{n}}\end{pmatrix}\:=\:? \\ $$

Question Number 205884    Answers: 2   Comments: 1

Question Number 205817    Answers: 2   Comments: 0

2^( x + log_2 3) = 12 β‡’ find: x = ?

$$\mathrm{2}^{\:\boldsymbol{\mathrm{x}}\:+\:\boldsymbol{\mathrm{log}}_{\mathrm{2}} \:\mathrm{3}} \:=\:\mathrm{12}\:\:\Rightarrow\:\:\mathrm{find}:\:\:\mathrm{x}\:=\:? \\ $$

Question Number 205790    Answers: 0   Comments: 0

Question Number 205789    Answers: 0   Comments: 0

Question Number 205772    Answers: 2   Comments: 0

Question Number 205770    Answers: 0   Comments: 0

If x,y,z>0 and xyz = 1 Prove that: ((((√2)x)^2 )/((1+xz)(1+xy))) + ((((√2)y)^2 )/((1+yz)(1+xy))) + ((((√2)z)^2 )/((1+xz)(1+yz))) β‰₯ (3/2)

$$\mathrm{If}\:\:\mathrm{x},\mathrm{y},\mathrm{z}>\mathrm{0}\:\:\mathrm{and}\:\:\mathrm{xyz}\:=\:\mathrm{1} \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{\left(\sqrt{\mathrm{2}}\mathrm{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xz}\right)\left(\mathrm{1}+\mathrm{xy}\right)}\:+\:\frac{\left(\sqrt{\mathrm{2}}\mathrm{y}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{yz}\right)\left(\mathrm{1}+\mathrm{xy}\right)}\:+\:\frac{\left(\sqrt{\mathrm{2}}\mathrm{z}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xz}\right)\left(\mathrm{1}+\mathrm{yz}\right)}\:\geqslant\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Question Number 205767    Answers: 1   Comments: 0

a,b,c βˆˆβ„œ^+ a+b+c=1 a^2 /(1+b+c) + b^2 /(1+a+c) + c^2 /(1+a+b)β‰₯k find k max. hint : inequality cauchy schwarz

$$ \\ $$$${a},{b},{c}\:\in\Re^{+} \:\: \\ $$$${a}+{b}+{c}=\mathrm{1} \\ $$$$\:\:\:{a}^{\mathrm{2}} /\left(\mathrm{1}+{b}+{c}\right)\:+\:{b}^{\mathrm{2}} /\left(\mathrm{1}+{a}+{c}\right)\:\:+\:{c}^{\mathrm{2}} /\left(\mathrm{1}+{a}+{b}\right)\geqslant{k} \\ $$$${find}\:\:\:{k}\:{max}. \\ $$$${hint}\::\:{inequality}\:{cauchy}\:{schwarz} \\ $$$$ \\ $$

Question Number 205746    Answers: 1   Comments: 0

Question Number 205733    Answers: 1   Comments: 0

If a,b,c∈R^+ and a+b+c=6 Prove that: ((a^2 βˆ’4)/(4a^2 βˆ’9a + 6)) + ((b^2 βˆ’4)/(4b^2 βˆ’9b + 6)) + ((c^2 βˆ’4)/(4c^2 βˆ’9c + 6)) ≀ 0

$$\mathrm{If}\:\:\mathrm{a},\mathrm{b},\mathrm{c}\in\mathbb{R}^{+} \:\:\mathrm{and}\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{6} \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} βˆ’\mathrm{4}}{\mathrm{4a}^{\mathrm{2}} βˆ’\mathrm{9a}\:+\:\mathrm{6}}\:+\:\frac{\mathrm{b}^{\mathrm{2}} βˆ’\mathrm{4}}{\mathrm{4b}^{\mathrm{2}} βˆ’\mathrm{9b}\:+\:\mathrm{6}}\:+\:\frac{\mathrm{c}^{\mathrm{2}} βˆ’\mathrm{4}}{\mathrm{4c}^{\mathrm{2}} βˆ’\mathrm{9c}\:+\:\mathrm{6}}\:\leqslant\:\mathrm{0} \\ $$

Question Number 205726    Answers: 1   Comments: 0

101 is chosen arbitrarily from the numbers 1,2,3,...,199,200. Prove that two of these selected numbers can be found such that one is divisible by the other.

$$ \\ $$101 is chosen arbitrarily from the numbers 1,2,3,...,199,200. Prove that two of these selected numbers can be found such that one is divisible by the other.

Question Number 205680    Answers: 1   Comments: 0

solve ⌊x βŒ‹ + ⌊ x^2 βŒ‹ = ⌊ x^3 βŒ‹

$$ \\ $$$$\:\:\:\:\:\:\:\:\:{solve}\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\lfloor{x}\:\rfloor\:+\:\lfloor\:{x}^{\mathrm{2}} \rfloor\:=\:\lfloor\:{x}^{\mathrm{3}} \:\rfloor \\ $$$$ \\ $$

Question Number 205672    Answers: 1   Comments: 0

Question Number 205671    Answers: 1   Comments: 0

Question Number 205670    Answers: 1   Comments: 0

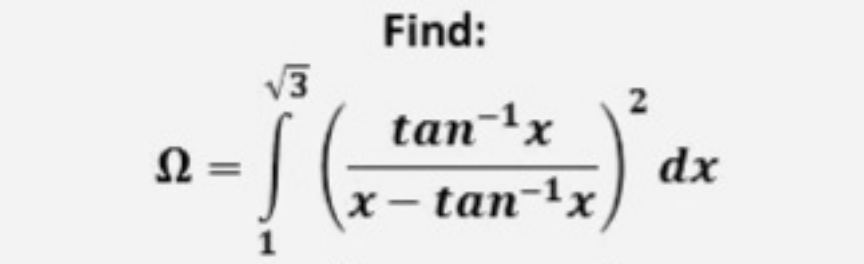
Question Number 205669    Answers: 1   Comments: 0

  Pg 41      Pg 42      Pg 43      Pg 44      Pg 45      Pg 46      Pg 47      Pg 48      Pg 49      Pg 50   

Terms of Service

Privacy Policy

Contact: [email protected]