Question and Answers Forum

AlgebraQuestion and Answers: Page 363

Question Number 19135 Answers: 1 Comments: 0

solve for x: 2^(∣x+2∣) −∣2^(x+1) −1∣=2^(x+1) +1

$${solve}\:{for}\:{x}: \\ $$$$\mathrm{2}^{\mid{x}+\mathrm{2}\mid} −\mid\mathrm{2}^{{x}+\mathrm{1}} −\mathrm{1}\mid=\mathrm{2}^{{x}+\mathrm{1}} +\mathrm{1} \\ $$

Question Number 19123 Answers: 1 Comments: 0

{ ((xf(x)−g(x)+h(x)=2x+1)),((f(x)−(2x−2)g(x)−3h(x)=x)),((ln (x)f(x)−(x−3)h(x)=1)) :} Find f(x),g(x),h(x)

Question Number 19121 Answers: 0 Comments: 0

Question Number 19101 Answers: 0 Comments: 3

A polynomial f(x) with rational coefficients leaves remainder 15, when divided by x − 3 and remainder 2x + 1, when divided by (x − 1)^2 . Find the remainder when f(x) is divided by (x − 3)(x − 1)^2 .

$$\mathrm{A}\:\mathrm{polynomial}\:{f}\left({x}\right)\:\mathrm{with}\:\mathrm{rational} \\ $$$$\mathrm{coefficients}\:\mathrm{leaves}\:\mathrm{remainder}\:\mathrm{15},\:\mathrm{when} \\ $$$$\mathrm{divided}\:\mathrm{by}\:{x}\:−\:\mathrm{3}\:\mathrm{and}\:\mathrm{remainder}\:\mathrm{2}{x}\:+\:\mathrm{1}, \\ $$$$\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} .\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{remainder}\:\mathrm{when}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by} \\ $$$$\left({x}\:−\:\mathrm{3}\right)\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} . \\ $$

Question Number 19095 Answers: 0 Comments: 3

Question Number 19063 Answers: 2 Comments: 0

find the possible values of x if ((8^x +27^x )/(12^x +18^x ))=(7/6)

$$\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{if} \\ $$$$\frac{\mathrm{8}^{\mathrm{x}} +\mathrm{27}^{\mathrm{x}} }{\mathrm{12}^{\mathrm{x}} +\mathrm{18}^{\mathrm{x}} }=\frac{\mathrm{7}}{\mathrm{6}} \\ $$

Question Number 19073 Answers: 0 Comments: 0

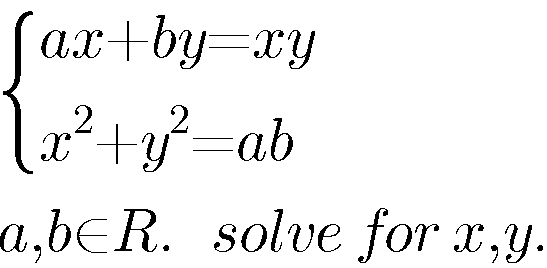
Question Number 18979 Answers: 0 Comments: 0

Question Number 18961 Answers: 1 Comments: 0

Find arg(z), z = i^i^i .

$$\mathrm{Find}\:\mathrm{arg}\left({z}\right),\:{z}\:=\:{i}^{{i}^{{i}} } . \\ $$

Question Number 18916 Answers: 0 Comments: 0

x^2 −7x+12<mod(x−4)

$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}<{mod}\left({x}−\mathrm{4}\right) \\ $$

Question Number 18864 Answers: 2 Comments: 1

Question Number 18885 Answers: 0 Comments: 0

Question Number 18798 Answers: 1 Comments: 0

Question Number 18779 Answers: 0 Comments: 2

If (1/(2x))+(1/2)((1/(2x))+(1/2)((1/(2x))+(1/2)((1/(2x))+......=y what does x equals? a)1/2 b)2/4 c)1 d)1/4

$$\mathrm{If}\:\:\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2x}}+......=\mathrm{y}\right.\right.\right. \\ $$$$\mathrm{what}\:\mathrm{does}\:\mathrm{x}\:\mathrm{equals}? \\ $$$$ \\ $$$$\left.\mathrm{a}\right)\mathrm{1}/\mathrm{2} \\ $$$$\left.\mathrm{b}\right)\mathrm{2}/\mathrm{4} \\ $$$$\left.\mathrm{c}\right)\mathrm{1} \\ $$$$\left.\mathrm{d}\right)\mathrm{1}/\mathrm{4} \\ $$

Question Number 18704 Answers: 1 Comments: 0

Question Number 18640 Answers: 1 Comments: 1

Question Number 18606 Answers: 0 Comments: 0

(1/3)+(3/(3×7))+(5/(3×7×11))+(7/(3×7×11×15))+...n terms

$$\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{3}×\mathrm{7}}+\frac{\mathrm{5}}{\mathrm{3}×\mathrm{7}×\mathrm{11}}+\frac{\mathrm{7}}{\mathrm{3}×\mathrm{7}×\mathrm{11}×\mathrm{15}}+...{n}\: \\ $$$$\:{terms} \\ $$

Question Number 19236 Answers: 1 Comments: 0

Question Number 18432 Answers: 1 Comments: 0

Find interval p so (p − 2)x^2 + 2px + p − 1 = 0 have negative roots

$$\mathrm{Find}\:\mathrm{interval}\:{p}\:\mathrm{so} \\ $$$$\left({p}\:−\:\mathrm{2}\right){x}^{\mathrm{2}} \:+\:\mathrm{2}{px}\:+\:{p}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{have}\:\mathrm{negative}\:\mathrm{roots} \\ $$

Question Number 18392 Answers: 1 Comments: 1

Question Number 18388 Answers: 1 Comments: 0

Solve simultaneously. x + y = 5 ....... (i) 5^x + y = 15 ...... (ii)

$$\mathrm{Solve}\:\mathrm{simultaneously}.\: \\ $$$$\mathrm{x}\:+\:\mathrm{y}\:=\:\mathrm{5}\:\:\:\:\:.......\:\left(\mathrm{i}\right) \\ $$$$\mathrm{5}^{\mathrm{x}} \:+\:\mathrm{y}\:=\:\mathrm{15}\:\:\:\:......\:\left(\mathrm{ii}\right) \\ $$

Question Number 18386 Answers: 1 Comments: 1

Prove that ((2 + (√5)))^(1/3) + ((2 − (√5)))^(1/3) is a rational number.

$$\mathrm{Prove}\:\mathrm{that}\:\sqrt[{\mathrm{3}}]{\mathrm{2}\:+\:\sqrt{\mathrm{5}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}\:−\:\sqrt{\mathrm{5}}}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{rational}\:\mathrm{number}. \\ $$

Question Number 18369 Answers: 1 Comments: 0

Prove that a^4 + b^4 + c^4 ≥ abc(a + b + c)

$$\mathrm{Prove}\:\mathrm{that}\:{a}^{\mathrm{4}} \:+\:{b}^{\mathrm{4}} \:+\:{c}^{\mathrm{4}} \:\geqslant\:{abc}\left({a}\:+\:{b}\:+\:{c}\right) \\ $$

Question Number 18299 Answers: 0 Comments: 2

x^x^x = 2, find x

$$\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \:=\:\mathrm{2},\:\:\:\:\:\:\mathrm{find}\:\:\mathrm{x} \\ $$

Question Number 18247 Answers: 0 Comments: 0

(((x+1)(x−1))/(x^2 +2x+3))

$$\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}} \\ $$

Question Number 18152 Answers: 0 Comments: 0

Pg 358 Pg 359 Pg 360 Pg 361 Pg 362 Pg 363 Pg 364 Pg 365 Pg 366 Pg 367

Contact: info@tinkutara.com