Question and Answers Forum

AlgebraQuestion and Answers: Page 355

Question Number 23953 Answers: 0 Comments: 4

find the nth term of the sequence 4, 9, 16, 45, 76 please help

$${find}\:{the}\:{nth}\:{term}\:{of}\:{the}\:{sequence} \\ $$$$\mathrm{4},\:\mathrm{9},\:\mathrm{16},\:\mathrm{45},\:\mathrm{76} \\ $$$$ \\ $$$${please}\:{help} \\ $$

Question Number 23928 Answers: 0 Comments: 4

Find^n C_1 − (1/2)^n C_2 + (1/3)^n C_3 − .... + (−1)^(n−1) (1/n) ∙^n C_n .

$$\mathrm{Find}\:^{{n}} {C}_{\mathrm{1}} \:−\:\frac{\mathrm{1}}{\mathrm{2}}\:^{{n}} {C}_{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\mathrm{3}}\:^{{n}} {C}_{\mathrm{3}} \:−\:....\:+ \\ $$$$\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{\mathrm{1}}{{n}}\:\centerdot\:^{{n}} {C}_{{n}} . \\ $$

Question Number 23884 Answers: 1 Comments: 0

If C_r stands for^n C_r = ((n!)/(r! n − r!)) and Σ_(r=1) ^n r.C_r ^2 = λ for n ≥ 2, then λ is divisible by (1) 3 (n − 1) (2) n + 1 (3) n (2n − 1) (4) n^2 + 1

$$\mathrm{If}\:{C}_{{r}} \:\mathrm{stands}\:\mathrm{for}\:^{{n}} {C}_{{r}} \:=\:\frac{{n}!}{{r}!\:{n}\:−\:{r}!}\:\mathrm{and} \\ $$$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}.{C}_{{r}} ^{\mathrm{2}} \:=\:\lambda\:\mathrm{for}\:{n}\:\geqslant\:\mathrm{2},\:\mathrm{then}\:\lambda\:\mathrm{is}\:\mathrm{divisible} \\ $$$$\mathrm{by} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{3}\:\left({n}\:−\:\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\:{n}\:+\:\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:{n}\:\left(\mathrm{2}{n}\:−\:\mathrm{1}\right) \\ $$$$\left(\mathrm{4}\right)\:{n}^{\mathrm{2}} \:+\:\mathrm{1} \\ $$

Question Number 23814 Answers: 1 Comments: 1

Question Number 23700 Answers: 0 Comments: 3

If (1 − x^3 )^n = Σ_(r=0) ^n a_r x^r (1 − x)^(3n−2r) , then the value of a_r , where n ∈ N is (1)^n C_r ∙3^r (2)^n C_(3r) (3)^n C_(r−1) 2^(r−1) (4)^n C_r 2^r

$$\mathrm{If}\:\left(\mathrm{1}\:−\:{x}^{\mathrm{3}} \right)^{{n}} \:=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{r}} {x}^{{r}} \left(\mathrm{1}\:−\:{x}\right)^{\mathrm{3}{n}−\mathrm{2}{r}} ,\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}_{{r}} ,\:\mathrm{where}\:{n}\:\in\:{N}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:^{{n}} {C}_{{r}} \centerdot\mathrm{3}^{{r}} \\ $$$$\left(\mathrm{2}\right)\:^{{n}} {C}_{\mathrm{3}{r}} \\ $$$$\left(\mathrm{3}\right)\:^{{n}} {C}_{{r}−\mathrm{1}} \mathrm{2}^{{r}−\mathrm{1}} \\ $$$$\left(\mathrm{4}\right)\:^{{n}} {C}_{{r}} \mathrm{2}^{{r}} \\ $$

Question Number 23687 Answers: 1 Comments: 0

Solve for x, y and z x^2 − yz = 1 .......... (i) y^2 − xz = 4 .......... (i) z^2 − xy = 9 .......... (i)

$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x},\:\mathrm{y}\:\mathrm{and}\:\mathrm{z} \\ $$$$\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{yz}\:=\:\mathrm{1}\:\:\:\:\:\:..........\:\left(\mathrm{i}\right) \\ $$$$\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{xz}\:=\:\mathrm{4}\:\:\:\:\:\:..........\:\left(\mathrm{i}\right) \\ $$$$\mathrm{z}^{\mathrm{2}} \:−\:\mathrm{xy}\:=\:\mathrm{9}\:\:\:\:\:\:..........\:\left(\mathrm{i}\right) \\ $$

Question Number 23682 Answers: 0 Comments: 0

Question Number 23644 Answers: 0 Comments: 0

Prove that Σ_(r=0) ^n r.^n C_r z^r = nz(1 + z)^(n−1)

$${Prove}\:{that}\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{r}.^{{n}} {C}_{{r}} \:{z}^{{r}} \:=\:{nz}\left(\mathrm{1}\:+\:{z}\right)^{{n}−\mathrm{1}} \\ $$

Question Number 23566 Answers: 1 Comments: 2

((a/b))^(log c) .((b/c))^(log a) .((c/a))^(log b) =1. make ((logc)/c) the subject of formula

$$\left(\frac{{a}}{{b}}\right)^{\mathrm{log}\:{c}} .\left(\frac{{b}}{{c}}\right)^{\mathrm{log}\:{a}} .\left(\frac{{c}}{{a}}\right)^{\mathrm{log}\:{b}} =\mathrm{1}. \\ $$$$ \\ $$$${make}\:\frac{{logc}}{{c}}\:{the}\:{subject}\:{of}\:{formula} \\ $$

Question Number 23537 Answers: 1 Comments: 8

Question Number 23479 Answers: 0 Comments: 0

Common solution. (d/dy)(u_x +u)+2x^2 y(u_x +u)=0.

$$\boldsymbol{\mathrm{Common}}\:\:\boldsymbol{\mathrm{solution}}. \\ $$$$\frac{\boldsymbol{\mathfrak{d}}}{\boldsymbol{\mathfrak{d}\mathrm{y}}}\left(\boldsymbol{\mathrm{u}}_{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{u}}\right)+\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{u}}_{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{u}}\right)=\mathrm{0}. \\ $$

Question Number 23471 Answers: 1 Comments: 0

Prove that ΣΣ_(0≤i<j≤n) ((1/(^n C_i )) + (1/(^n C_j ))) = Σ_(r=0) ^(n−1) ((n − r)/(^n C_r )) + Σ_(r=1) ^n (r/(^n C_r ))

$${Prove}\:{that} \\ $$$$\underset{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} {\Sigma\Sigma}\left(\frac{\mathrm{1}}{\:^{{n}} {C}_{{i}} }\:+\:\frac{\mathrm{1}}{\:^{{n}} {C}_{{j}} }\right)\:=\:\underset{{r}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{n}\:−\:{r}}{\:^{{n}} {C}_{{r}} }\:+\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{r}}{\:^{{n}} {C}_{{r}} } \\ $$

Question Number 23357 Answers: 0 Comments: 0

Prove that (1/(m!))C_0 +(n/((m+1)!))C_1 +((n(n−1))/((m+2)!))C_2 +...+((n(n−1)...2.1)/((m+n)!))C_n = (((m+n+1)(m+n+2)...(m+2n))/((m+n)!)).

$${Prove}\:{that}\:\frac{\mathrm{1}}{{m}!}{C}_{\mathrm{0}} +\frac{{n}}{\left({m}+\mathrm{1}\right)!}{C}_{\mathrm{1}} +\frac{{n}\left({n}−\mathrm{1}\right)}{\left({m}+\mathrm{2}\right)!}{C}_{\mathrm{2}} \\ $$$$+...+\frac{{n}\left({n}−\mathrm{1}\right)...\mathrm{2}.\mathrm{1}}{\left({m}+{n}\right)!}{C}_{{n}} = \\ $$$$\frac{\left({m}+{n}+\mathrm{1}\right)\left({m}+{n}+\mathrm{2}\right)...\left({m}+\mathrm{2}{n}\right)}{\left({m}+{n}\right)!}. \\ $$

Question Number 23334 Answers: 1 Comments: 3

Question Number 23323 Answers: 0 Comments: 1

Question Number 23250 Answers: 0 Comments: 0

If (1 + x)^n = C_0 + C_1 x + C_2 x^2 + C_3 x^3 + ... + C_n x^n , then prove that ΣΣ_(0≤i<j≤n) ((i/(^n C_i )) + (j/(^n C_j ))) = (n^2 /2)(Σ_(r=0) ^n (1/(^n C_r ))).

$${If}\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} \:=\:{C}_{\mathrm{0}} \:+\:{C}_{\mathrm{1}} {x}\:+\:{C}_{\mathrm{2}} {x}^{\mathrm{2}} \:+\:{C}_{\mathrm{3}} {x}^{\mathrm{3}} \\ $$$$+\:...\:+\:{C}_{{n}} {x}^{{n}} ,\:{then}\:{prove}\:{that} \\ $$$$\underset{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} {\Sigma\Sigma}\left(\frac{{i}}{\:^{{n}} {C}_{{i}} }\:+\:\frac{{j}}{\:^{{n}} {C}_{{j}} }\right)\:=\:\frac{{n}^{\mathrm{2}} }{\mathrm{2}}\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:^{{n}} {C}_{{r}} }\right). \\ $$

Question Number 23208 Answers: 1 Comments: 0

Is it possible to find how many real roots exist in the equation x^4 + ∣x∣ = 3 without find all the value of x?

$$\mathrm{Is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{find}\:\mathrm{how}\:\mathrm{many}\:\mathrm{real}\:\mathrm{roots}\: \\ $$$$\mathrm{exist}\:\mathrm{in}\:\mathrm{the}\:\mathrm{equation} \\ $$$${x}^{\mathrm{4}} \:+\:\mid{x}\mid\:=\:\mathrm{3} \\ $$$$\mathrm{without}\:\mathrm{find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:{x}? \\ $$

Question Number 23096 Answers: 0 Comments: 1

Solve: 3^(x ) = ((27)/x) + 18

$$\mathrm{Solve}:\:\:\mathrm{3}^{\mathrm{x}\:} =\:\frac{\mathrm{27}}{\mathrm{x}}\:+\:\mathrm{18} \\ $$

Question Number 23000 Answers: 0 Comments: 0

Let n be a positive integer and p_1 , p_2 , ..., p_n be n prime numbers all larger than 5 such that 6 divides p_1 ^2 + p_2 ^2 + ... + p_n ^2 . Prove that 6 divides n.

$$\mathrm{Let}\:{n}\:\mathrm{be}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{and}\:{p}_{\mathrm{1}} ,\:{p}_{\mathrm{2}} , \\ $$$$...,\:{p}_{{n}} \:\mathrm{be}\:{n}\:\mathrm{prime}\:\mathrm{numbers}\:\mathrm{all}\:\mathrm{larger} \\ $$$$\mathrm{than}\:\mathrm{5}\:\mathrm{such}\:\mathrm{that}\:\mathrm{6}\:\mathrm{divides}\:{p}_{\mathrm{1}} ^{\mathrm{2}} \:+\:{p}_{\mathrm{2}} ^{\mathrm{2}} \:+\:...\:+ \\ $$$${p}_{{n}} ^{\mathrm{2}} .\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{6}\:\mathrm{divides}\:{n}. \\ $$

Question Number 22945 Answers: 0 Comments: 0

Question Number 22856 Answers: 0 Comments: 1

solve: sin(x)=2, x∈C

$$\mathrm{solve}:\:\mathrm{sin}\left({x}\right)=\mathrm{2},\:\:\:{x}\in\mathbb{C} \\ $$

Question Number 22768 Answers: 1 Comments: 2

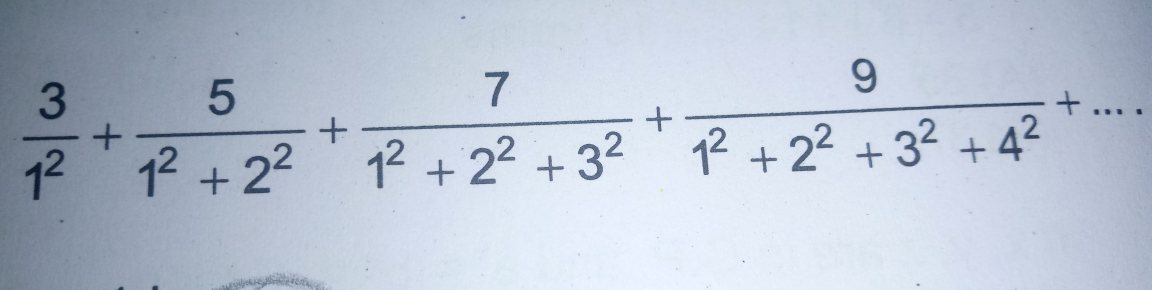
Question Number 22739 Answers: 0 Comments: 0

If (1 + x)^n = C_0 + C_1 x + C_2 x^2 + C_3 x^3 + ... + C_n x^n , Prove that ΣΣ_(0≤i<j≤n) (i + j)C_i C_j = n(2^(2n−1) − (1/2)^(2n) C_n )

Question Number 22701 Answers: 2 Comments: 0

Question Number 22618 Answers: 1 Comments: 0

If (1 + x)^n = C_0 + C_1 x + C_2 x^2 + C_3 x^3 + ... + C_n x^n , prove that (2^2 /(1.2))C_0 + (2^3 /(2.3))C_1 + (2^4 /(3.4))C_2 + ... + (2^(n+2) /((n + 1)(n + 2)))C_n = ((3^(n+2) − 2n − 5)/((n + 1)(n + 2)))

$${If}\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} \:=\:{C}_{\mathrm{0}} \:+\:{C}_{\mathrm{1}} {x}\:+\:{C}_{\mathrm{2}} {x}^{\mathrm{2}} \:+\:{C}_{\mathrm{3}} {x}^{\mathrm{3}} \\ $$$$+\:...\:+\:{C}_{{n}} {x}^{{n}} ,\:{prove}\:{that} \\ $$$$\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1}.\mathrm{2}}{C}_{\mathrm{0}} \:+\:\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{2}.\mathrm{3}}{C}_{\mathrm{1}} \:+\:\frac{\mathrm{2}^{\mathrm{4}} }{\mathrm{3}.\mathrm{4}}{C}_{\mathrm{2}} \:+\:...\:+ \\ $$$$\frac{\mathrm{2}^{{n}+\mathrm{2}} }{\left({n}\:+\:\mathrm{1}\right)\left({n}\:+\:\mathrm{2}\right)}{C}_{{n}} \:=\:\frac{\mathrm{3}^{{n}+\mathrm{2}} \:−\:\mathrm{2}{n}\:−\:\mathrm{5}}{\left({n}\:+\:\mathrm{1}\right)\left({n}\:+\:\mathrm{2}\right)} \\ $$

Question Number 22640 Answers: 0 Comments: 0

With usual notation, show that (C_0 /x) − (C_1 /(x+1)) + (C_2 /(x+2)) − .... + (−1)^n (C_n /(x+n))= ((n!)/(x(x + 1)(x + 2)....(x + n)))

$${With}\:{usual}\:{notation},\:{show}\:{that} \\ $$$$\frac{{C}_{\mathrm{0}} }{{x}}\:−\:\frac{{C}_{\mathrm{1}} }{{x}+\mathrm{1}}\:+\:\frac{{C}_{\mathrm{2}} }{{x}+\mathrm{2}}\:−\:....\:+\:\left(−\mathrm{1}\right)^{{n}} \frac{{C}_{{n}} }{{x}+{n}}= \\ $$$$\frac{{n}!}{{x}\left({x}\:+\:\mathrm{1}\right)\left({x}\:+\:\mathrm{2}\right)....\left({x}\:+\:{n}\right)} \\ $$

Pg 350 Pg 351 Pg 352 Pg 353 Pg 354 Pg 355 Pg 356 Pg 357 Pg 358 Pg 359

Contact: info@tinkutara.com