
AlgebraQuestion and Answers: Page 349
Question Number 28370 Answers: 0 Comments: 1
Question Number 28369 Answers: 0 Comments: 0
Question Number 28368 Answers: 0 Comments: 0
Question Number 28367 Answers: 0 Comments: 0
Question Number 28366 Answers: 0 Comments: 0
Question Number 28364 Answers: 0 Comments: 0
Question Number 28363 Answers: 1 Comments: 0
Question Number 28327 Answers: 1 Comments: 0
Question Number 28320 Answers: 0 Comments: 3
Question Number 28319 Answers: 2 Comments: 0
Question Number 28312 Answers: 1 Comments: 0
Question Number 28311 Answers: 0 Comments: 0
Question Number 28313 Answers: 0 Comments: 0
Question Number 28288 Answers: 2 Comments: 0
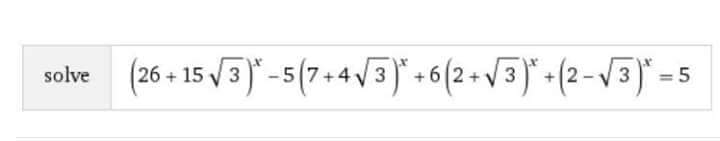
Question Number 28275 Answers: 0 Comments: 2
Question Number 28267 Answers: 1 Comments: 1
Question Number 28265 Answers: 0 Comments: 0
Question Number 28264 Answers: 0 Comments: 0
Question Number 28219 Answers: 0 Comments: 4

Question Number 28211 Answers: 0 Comments: 6

Question Number 28190 Answers: 1 Comments: 2

Question Number 28189 Answers: 0 Comments: 2

Question Number 28188 Answers: 0 Comments: 0

Question Number 28174 Answers: 0 Comments: 2
Question Number 28166 Answers: 0 Comments: 0
Question Number 28165 Answers: 0 Comments: 0
Pg 344 Pg 345 Pg 346 Pg 347 Pg 348 Pg 349 Pg 350 Pg 351 Pg 352 Pg 353
