
AlgebraQuestion and Answers: Page 347
Question Number 28921 Answers: 1 Comments: 0

Question Number 28857 Answers: 1 Comments: 0

Question Number 28856 Answers: 0 Comments: 0

Question Number 28739 Answers: 1 Comments: 0
Question Number 28642 Answers: 0 Comments: 0
Question Number 28554 Answers: 2 Comments: 0
Question Number 28546 Answers: 0 Comments: 0
Question Number 28544 Answers: 0 Comments: 2
Question Number 28534 Answers: 0 Comments: 1
Question Number 28533 Answers: 0 Comments: 1
Question Number 28532 Answers: 0 Comments: 1
Question Number 28506 Answers: 0 Comments: 3
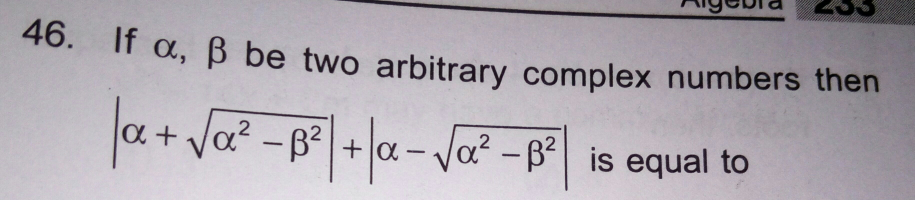
Question Number 28435 Answers: 0 Comments: 0
Question Number 28434 Answers: 0 Comments: 0
Question Number 28433 Answers: 0 Comments: 0
Question Number 28432 Answers: 0 Comments: 1
Question Number 28393 Answers: 0 Comments: 0
Question Number 28382 Answers: 1 Comments: 0
Question Number 28381 Answers: 0 Comments: 0

Question Number 28375 Answers: 1 Comments: 0
Question Number 28372 Answers: 0 Comments: 0
Question Number 28371 Answers: 0 Comments: 1
Question Number 28370 Answers: 0 Comments: 1
Question Number 28369 Answers: 0 Comments: 0
Question Number 28368 Answers: 0 Comments: 0
Question Number 28367 Answers: 0 Comments: 0
Pg 342 Pg 343 Pg 344 Pg 345 Pg 346 Pg 347 Pg 348 Pg 349 Pg 350 Pg 351
