
AlgebraQuestion and Answers: Page 345
Question Number 30860 Answers: 1 Comments: 0
Question Number 30849 Answers: 0 Comments: 5
Question Number 30745 Answers: 0 Comments: 0
Question Number 30744 Answers: 0 Comments: 0
Question Number 30743 Answers: 0 Comments: 1
Question Number 30742 Answers: 0 Comments: 0
Question Number 30739 Answers: 0 Comments: 0
Question Number 30627 Answers: 1 Comments: 0
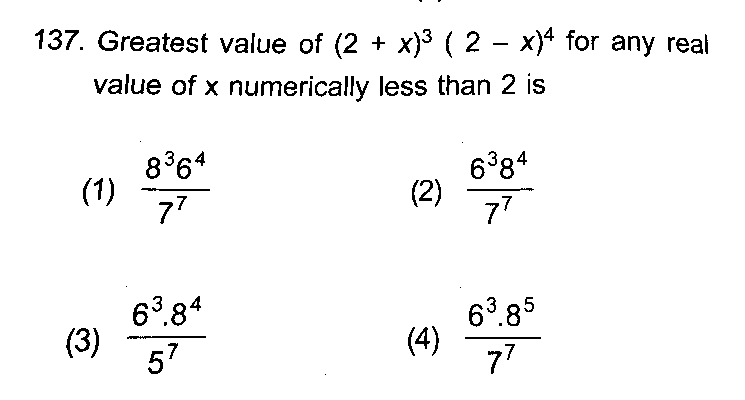
Question Number 30600 Answers: 0 Comments: 0
Question Number 30599 Answers: 0 Comments: 1
Question Number 30598 Answers: 0 Comments: 1
Question Number 30597 Answers: 0 Comments: 0
Question Number 30596 Answers: 0 Comments: 0
Question Number 30594 Answers: 0 Comments: 0
Question Number 30593 Answers: 1 Comments: 0
Question Number 30592 Answers: 1 Comments: 0
Question Number 30590 Answers: 1 Comments: 0
$${decompose}\:{sur}\:{R}\left[{x}\right]\:\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:−\mathrm{1}. \\ $$
Question Number 30589 Answers: 0 Comments: 0
Question Number 30588 Answers: 0 Comments: 0
Question Number 30587 Answers: 0 Comments: 0
Question Number 30586 Answers: 0 Comments: 0
Question Number 30583 Answers: 0 Comments: 0
Question Number 30582 Answers: 0 Comments: 0
Question Number 30581 Answers: 0 Comments: 0
Question Number 30579 Answers: 0 Comments: 0
Question Number 30578 Answers: 0 Comments: 0
Pg 340 Pg 341 Pg 342 Pg 343 Pg 344 Pg 345 Pg 346 Pg 347 Pg 348 Pg 349
