
AlgebraQuestion and Answers: Page 341
Question Number 32334 Answers: 0 Comments: 1
Question Number 32333 Answers: 0 Comments: 1
Question Number 32332 Answers: 0 Comments: 0
Question Number 32331 Answers: 0 Comments: 0
Question Number 32330 Answers: 0 Comments: 1
Question Number 32326 Answers: 0 Comments: 0
Question Number 32242 Answers: 1 Comments: 0
Question Number 32239 Answers: 1 Comments: 0
Question Number 32208 Answers: 0 Comments: 0

Question Number 32203 Answers: 0 Comments: 5
Question Number 32184 Answers: 1 Comments: 0
Question Number 32181 Answers: 1 Comments: 1
Question Number 32160 Answers: 1 Comments: 0
Question Number 32159 Answers: 1 Comments: 2
Question Number 32142 Answers: 0 Comments: 0
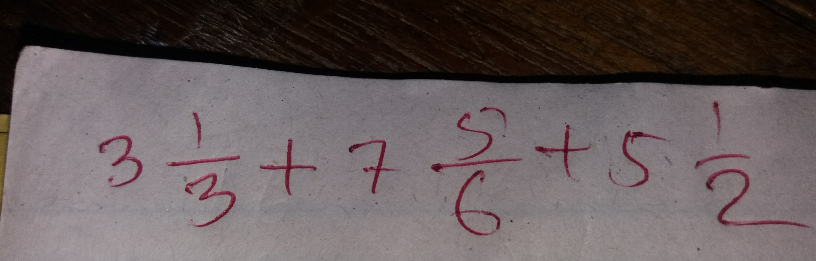
Question Number 32132 Answers: 0 Comments: 0
$$\int\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right){ln}\left({x}\right)}{dx}=? \\ $$
Question Number 32110 Answers: 1 Comments: 0
Question Number 32099 Answers: 1 Comments: 0

Question Number 32094 Answers: 0 Comments: 0
Question Number 32049 Answers: 2 Comments: 0
Question Number 32047 Answers: 0 Comments: 1

Question Number 32002 Answers: 1 Comments: 0
Question Number 31991 Answers: 0 Comments: 1
Question Number 31990 Answers: 1 Comments: 3
Question Number 31963 Answers: 0 Comments: 0
Question Number 31927 Answers: 1 Comments: 0
Pg 336 Pg 337 Pg 338 Pg 339 Pg 340 Pg 341 Pg 342 Pg 343 Pg 344 Pg 345
