
AlgebraQuestion and Answers: Page 336
Question Number 36909 Answers: 0 Comments: 0
Question Number 36905 Answers: 0 Comments: 0
Question Number 36904 Answers: 0 Comments: 1
Question Number 36903 Answers: 0 Comments: 0
Question Number 36871 Answers: 0 Comments: 0

Question Number 36844 Answers: 1 Comments: 0
Question Number 36843 Answers: 1 Comments: 1
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}^{{x}^{{x}^{.....} } } \right) \\ $$
Question Number 36828 Answers: 0 Comments: 7

Question Number 36699 Answers: 0 Comments: 0

Question Number 36696 Answers: 0 Comments: 0
Question Number 36692 Answers: 2 Comments: 1
Question Number 36691 Answers: 0 Comments: 2

Question Number 36676 Answers: 1 Comments: 3
Question Number 36660 Answers: 1 Comments: 0
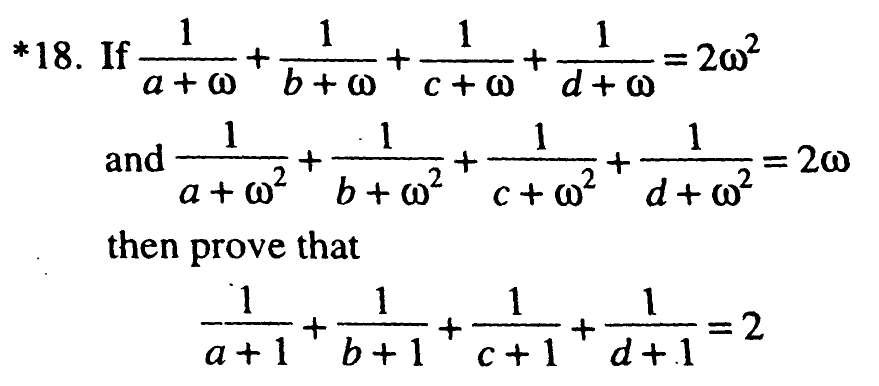
Question Number 36437 Answers: 0 Comments: 3
$${simplify}\:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:\:\frac{{C}_{{n}} ^{{k}} }{{k}+\mathrm{1}} \\ $$
Question Number 36359 Answers: 0 Comments: 0
Question Number 36352 Answers: 0 Comments: 1
Question Number 36344 Answers: 0 Comments: 3

Question Number 36259 Answers: 4 Comments: 0
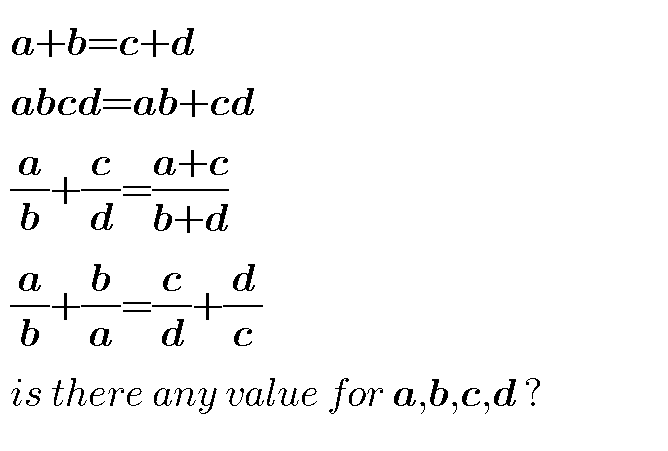
Question Number 36221 Answers: 2 Comments: 1
Question Number 36219 Answers: 0 Comments: 2
Question Number 36207 Answers: 0 Comments: 4
Question Number 36154 Answers: 0 Comments: 0
Question Number 36153 Answers: 0 Comments: 1
$$\frac{\left({x}+{yi}−\mathrm{2}\right)^{\mathrm{2}} }{{x}−{yi}+\mathrm{1}} \\ $$
Question Number 36132 Answers: 0 Comments: 7
Question Number 36126 Answers: 0 Comments: 4
Pg 331 Pg 332 Pg 333 Pg 334 Pg 335 Pg 336 Pg 337 Pg 338 Pg 339 Pg 340
