Question and Answers Forum

Find the maximum common divisor of the folllwing polynomials: •f(x)=x^4 +5x^3 −4x^2 −2x and g(x)=−3x^4 −x^3 +4x^2 in Q[x]. •f(x)=2x^2 −2 and g(x)=x^4 −3x^3 +x^2 +3x−2 in R[x]

$${Find}\:{the}\:{maximum}\:{common}\:{divisor} \\ $$$${of}\:{the}\:{folllwing}\:{polynomials}: \\ $$$$\bullet{f}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}{x}\:{and}\: \\ $$$${g}\left({x}\right)=−\mathrm{3}{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} \:{in}\:{Q}\left[{x}\right]. \\ $$$$\bullet{f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}\:{and}\:{g}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\:{in}\:{R}\left[{x}\right] \\ $$

Question Number 49237 Answers: 0 Comments: 0

Find a polynomial f(x)∈Q[x] such that its main coefficient is 1 and ((√2)+(√3))∈V(f)

$${Find}\:{a}\:{polynomial}\:{f}\left({x}\right)\in{Q}\left[{x}\right]\:{such} \\ $$$${that}\:{its}\:{main}\:{coefficient}\:{is}\:\mathrm{1}\:{and}\: \\ $$$$\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)\in{V}\left({f}\right) \\ $$

Question Number 49235 Answers: 0 Comments: 0

Let A a conmutative ring with 1 (not necessarily a whole domain). Study the structure that has A(x) with the usual operations Is it a ring always? Is it a whole domain? How are the units?

$${Let}\:{A}\:{a}\:{conmutative}\:{ring}\:{with}\:\mathrm{1}\: \\ $$$$\left({not}\:{necessarily}\:{a}\:{whole}\:{domain}\right). \\ $$$${Study}\:{the}\:{structure}\:{that}\:{has}\:{A}\left({x}\right)\: \\ $$$${with}\:{the}\:{usual}\:{operations} \\ $$$${Is}\:{it}\:{a}\:{ring}\:{always}? \\ $$$${Is}\:{it}\:{a}\:{whole}\:{domain}? \\ $$$${How}\:{are}\:{the}\:{units}? \\ $$

Question Number 49229 Answers: 0 Comments: 4

x^2 −y^2

$$\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} \\ $$

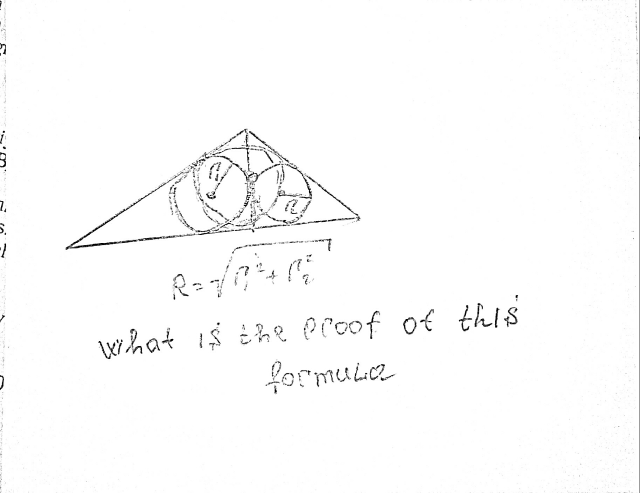
Question Number 49220 Answers: 0 Comments: 2

(1+x−2x^2 )^8 =?

$$\left(\mathrm{1}+\mathrm{x}−\mathrm{2x}^{\mathrm{2}} \:\right)^{\mathrm{8}} =? \\ $$

Question Number 49202 Answers: 2 Comments: 4

1) If ω is an imaginary fifth root of unity, then find value of log _2 ∣1+ω+ω^2 +ω^3 −(1/ω)∣ ? 2) Find value of : (i+(√3))^(100) +(i−(√3))^(100) +2^(100) ?

$$\left.\mathrm{1}\right)\:{If}\:\omega\:{is}\:{an}\:{imaginary}\:{fifth}\:{root}\:{of} \\ $$$${unity},\:{then}\:{find}\:{value}\:{of}\: \\ $$$$\mathrm{log}\:_{\mathrm{2}} \:\mid\mathrm{1}+\omega+\omega^{\mathrm{2}} +\omega^{\mathrm{3}} −\frac{\mathrm{1}}{\omega}\mid\:? \\ $$$$\left.\mathrm{2}\right)\:{Find}\:{value}\:{of}\:: \\ $$$$\left({i}+\sqrt{\mathrm{3}}\right)^{\mathrm{100}} +\left({i}−\sqrt{\mathrm{3}}\right)^{\mathrm{100}} +\mathrm{2}^{\mathrm{100}} \:? \\ $$

Question Number 49200 Answers: 2 Comments: 1

1)Find the area of the triangle formed by roots of cubic equation (z+αb)^3 =α^3_ (α≠0). 2) Find product of all possible values of ((1/2)+(((√3)i)/2))^(3/4) .

$$\left.\mathrm{1}\right){Find}\:{the}\:{area}\:{of}\:{the}\:{triangle}\:{formed} \\ $$$${by}\:{roots}\:{of}\:{cubic}\:{equation} \\ $$$$\left({z}+\alpha{b}\right)^{\mathrm{3}} =\alpha^{\mathrm{3}_{} } \:\:\left(\alpha\neq\mathrm{0}\right). \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{Find}\:{product}\:{of}\:{all}\:{possible}\:{values} \\ $$$${of}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \:. \\ $$

Question Number 49188 Answers: 1 Comments: 1

solve for x,y,z∈R. x^2 +yz=1 y^2 +xz=2 z^2 +xy=3

$${solve}\:{for}\:{x},{y},{z}\in{R}. \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{yz}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\boldsymbol{\mathrm{xz}}=\mathrm{2} \\ $$$$\boldsymbol{\mathrm{z}}^{\mathrm{2}} +\boldsymbol{\mathrm{xy}}=\mathrm{3} \\ $$

Question Number 49186 Answers: 1 Comments: 4

please help... There is : 21x^2 − 21p x + 49p − 7 = 0 whose roots u and v. If u and v are not ∈Z , and u,v ≥ 1. find the value of u + v !

$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{help}}... \\ $$$$ \\ $$$$\mathrm{There}\:\mathrm{is}\::\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{21}\boldsymbol{{x}}^{\mathrm{2}} \:−\:\mathrm{21}\boldsymbol{{p}}\:\boldsymbol{{x}}\:+\:\mathrm{49}\boldsymbol{{p}}\:−\:\mathrm{7}\:=\:\mathrm{0} \\ $$$$\mathrm{whose}\:\mathrm{roots}\:\boldsymbol{{u}}\:\mathrm{and}\:\boldsymbol{{v}}.\:\mathrm{If}\:\boldsymbol{{u}}\:\mathrm{and}\:\boldsymbol{{v}}\:\mathrm{are}\:\mathrm{not}\:\in\mathbb{Z}\:,\: \\ $$$$\mathrm{and}\:\boldsymbol{{u}},\boldsymbol{{v}}\:\geqslant\:\mathrm{1}. \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\boldsymbol{{u}}\:+\:\boldsymbol{{v}}\:! \\ $$$$ \\ $$

Question Number 49177 Answers: 1 Comments: 0

If ∣z_1 −z_2 ∣ = ∣z_1 ∣+∣z_2 ∣ , then prove that arg((z_1 /z_2 ))=π .

$${If}\:\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid\:=\:\mid{z}_{\mathrm{1}} \mid+\mid{z}_{\mathrm{2}} \mid\:,\:{then}\:{prove}\: \\ $$$${that}\:{arg}\left(\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\right)=\pi\:. \\ $$

Question Number 49169 Answers: 1 Comments: 0

Find the least positive integer n such that (((2i)/(1+i)))^n is a +ve integer ?

$${Find}\:{the}\:{least}\:{positive}\:{integer}\:{n}\:{such} \\ $$$${that}\:\left(\frac{\mathrm{2}{i}}{\mathrm{1}+{i}}\right)^{{n}} {is}\:{a}\:+{ve}\:{integer}\:? \\ $$

Question Number 49174 Answers: 1 Comments: 1

If z_1 ,z_2 and z_3 ,z_(4 ) are two pairs of conjugate complex numbers , then find value of arg((z_1 /z_4 ))+arg((z_2 /z_3 )) ?

$${If}\:{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} \:{and}\:{z}_{\mathrm{3}} ,{z}_{\mathrm{4}\:} {are}\:{two}\:{pairs}\:{of}\: \\ $$$${conjugate}\:{complex}\:{numbers}\:,\:{then}\: \\ $$$${find}\:{value}\:{of}\:{arg}\left(\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{4}} }\right)+{arg}\left(\frac{{z}_{\mathrm{2}} }{{z}_{\mathrm{3}} }\right)\:? \\ $$

Question Number 49151 Answers: 1 Comments: 0

Let z is complex number satisfying the equation z^2 −(3+i)z+m+2i=0, where mεR. Suppose the equation has a real root, then find the non real root?

$${Let}\:{z}\:{is}\:{complex}\:{number}\:{satisfying} \\ $$$${the}\:{equation}\:{z}^{\mathrm{2}} −\left(\mathrm{3}+{i}\right){z}+{m}+\mathrm{2}{i}=\mathrm{0}, \\ $$$${where}\:{m}\epsilon{R}.\:{Suppose}\:{the}\:{equation} \\ $$$${has}\:{a}\:{real}\:{root},\:{then}\:{find}\:{the}\:{non}\:{real}\:{root}? \\ $$

Question Number 49147 Answers: 1 Comments: 0

Question Number 49123 Answers: 1 Comments: 1

If a^3 −a−1=0 then find the valueof a^4 +a^3 −a^2 −2a+1

$$\mathrm{If} \\ $$$$\mathrm{a}^{\mathrm{3}} −\mathrm{a}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{valueof} \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{a}^{\mathrm{3}} −\mathrm{a}^{\mathrm{2}} −\mathrm{2a}+\mathrm{1} \\ $$

Question Number 48795 Answers: 1 Comments: 1

Find the sum: ^(30) C_0 .5^(100) −^(30) C_1 .5^(98) .3^3 +^(30) C_2 .5^(96) .3^6 − ...=?

$${Find}\:{the}\:{sum}: \\ $$$$\:^{\mathrm{30}} {C}_{\mathrm{0}} .\mathrm{5}^{\mathrm{100}} −^{\mathrm{30}} {C}_{\mathrm{1}} .\mathrm{5}^{\mathrm{98}} .\mathrm{3}^{\mathrm{3}} +^{\mathrm{30}} {C}_{\mathrm{2}} .\mathrm{5}^{\mathrm{96}} .\mathrm{3}^{\mathrm{6}} −\:...=? \\ $$

Question Number 48687 Answers: 0 Comments: 0

f(x)=sin (x) f(x)+f′((1/x))=(1/2)(√2) find x?

$${f}\left({x}\right)=\mathrm{sin}\:\left({x}\right) \\ $$$${f}\left({x}\right)+{f}'\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}} \\ $$$$\mathrm{find}\:{x}? \\ $$

Question Number 48705 Answers: 3 Comments: 2

Q.1→ Coefficient of a^8 b^4 c^9 d^9 in expansion of (abc+abd+acd+bcd)^(10) =? Q.2→ Coefficient of (1/x) in expansion of (1+x)^n (1+(1/x))^n =? Q.3→ If x^m occurs in expansion of (x+(1/x^2 ))^(2n) , then its coefficient=?

$${Q}.\mathrm{1}\rightarrow \\ $$$${Coefficient}\:{of}\:{a}^{\mathrm{8}} {b}^{\mathrm{4}} {c}^{\mathrm{9}} {d}^{\mathrm{9}} \:{in}\:{expansion} \\ $$$${of}\:\left({abc}+{abd}+{acd}+{bcd}\right)^{\mathrm{10}} \:=? \\ $$$$ \\ $$$${Q}.\mathrm{2}\rightarrow \\ $$$${Coefficient}\:{of}\:\frac{\mathrm{1}}{{x}}\:{in}\:{expansion}\:{of} \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{n}} =? \\ $$$$ \\ $$$${Q}.\mathrm{3}\rightarrow \\ $$$${If}\:{x}^{{m}} \:{occurs}\:{in}\:{expansion}\:{of}\: \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}{n}} ,\:{then}\:{its}\:{coefficient}=? \\ $$

Question Number 48678 Answers: 0 Comments: 0

Question Number 48675 Answers: 2 Comments: 0

Find remainder when 27^(40) is divided by 12 ?

$${Find}\:{remainder}\:{when}\:\mathrm{27}^{\mathrm{40}} \:{is}\:{divided} \\ $$$${by}\:\mathrm{12}\:? \\ $$

Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 Pg 328

Contact: info@tinkutara.com