
AlgebraQuestion and Answers: Page 312
Question Number 60816 Answers: 1 Comments: 0
Question Number 60745 Answers: 4 Comments: 5

Question Number 60734 Answers: 1 Comments: 4
Question Number 60723 Answers: 0 Comments: 10
Question Number 60705 Answers: 1 Comments: 0
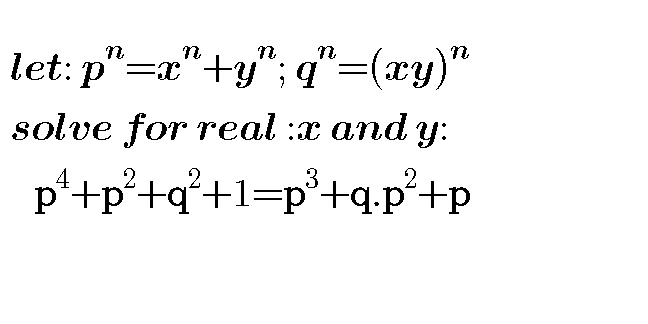
Question Number 60533 Answers: 1 Comments: 2
Question Number 60501 Answers: 1 Comments: 1
Question Number 60500 Answers: 0 Comments: 2
Question Number 60475 Answers: 1 Comments: 0

Question Number 60453 Answers: 0 Comments: 0

Question Number 60445 Answers: 2 Comments: 1

Question Number 60416 Answers: 0 Comments: 0
Question Number 60406 Answers: 1 Comments: 0
Question Number 60330 Answers: 0 Comments: 1

Question Number 60255 Answers: 0 Comments: 0
Question Number 60175 Answers: 0 Comments: 2
Question Number 60156 Answers: 3 Comments: 2
Question Number 60056 Answers: 1 Comments: 1

Question Number 60052 Answers: 0 Comments: 0
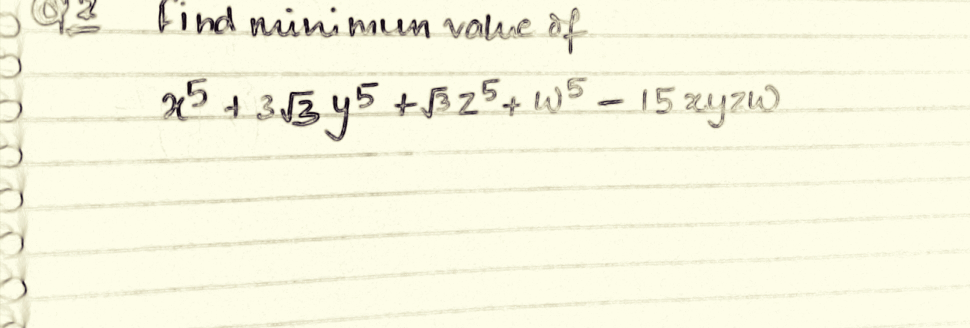
Question Number 60039 Answers: 2 Comments: 3
Question Number 59977 Answers: 1 Comments: 0
Question Number 59929 Answers: 0 Comments: 0
Question Number 59833 Answers: 1 Comments: 0

Question Number 59678 Answers: 0 Comments: 0
Question Number 59615 Answers: 1 Comments: 0
$$\mathrm{6}+\left(\frac{\mathrm{1}}{\mathrm{5}}×\mathrm{7}\right) \\ $$
Question Number 59614 Answers: 1 Comments: 0
$$\mathrm{1}\frac{\mathrm{1}}{\mathrm{7}}+\mathrm{1}\frac{\mathrm{1}}{\mathrm{14}} \\ $$
Pg 307 Pg 308 Pg 309 Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315 Pg 316
