
AlgebraQuestion and Answers: Page 307
Question Number 64112 Answers: 2 Comments: 1

Question Number 64066 Answers: 1 Comments: 0
Question Number 64061 Answers: 1 Comments: 0
Question Number 63958 Answers: 0 Comments: 1
Question Number 63945 Answers: 0 Comments: 1
Question Number 63930 Answers: 0 Comments: 0

Question Number 63893 Answers: 0 Comments: 1
Question Number 63858 Answers: 1 Comments: 0
Question Number 63803 Answers: 1 Comments: 4

Question Number 63784 Answers: 0 Comments: 6
Question Number 63678 Answers: 0 Comments: 1

Question Number 63642 Answers: 2 Comments: 1
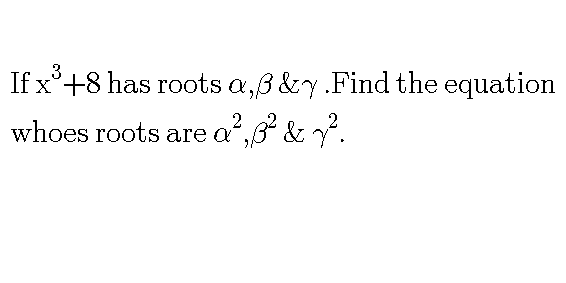
Question Number 63639 Answers: 0 Comments: 0

Question Number 63602 Answers: 2 Comments: 0
Question Number 63574 Answers: 0 Comments: 12
Question Number 63573 Answers: 0 Comments: 0
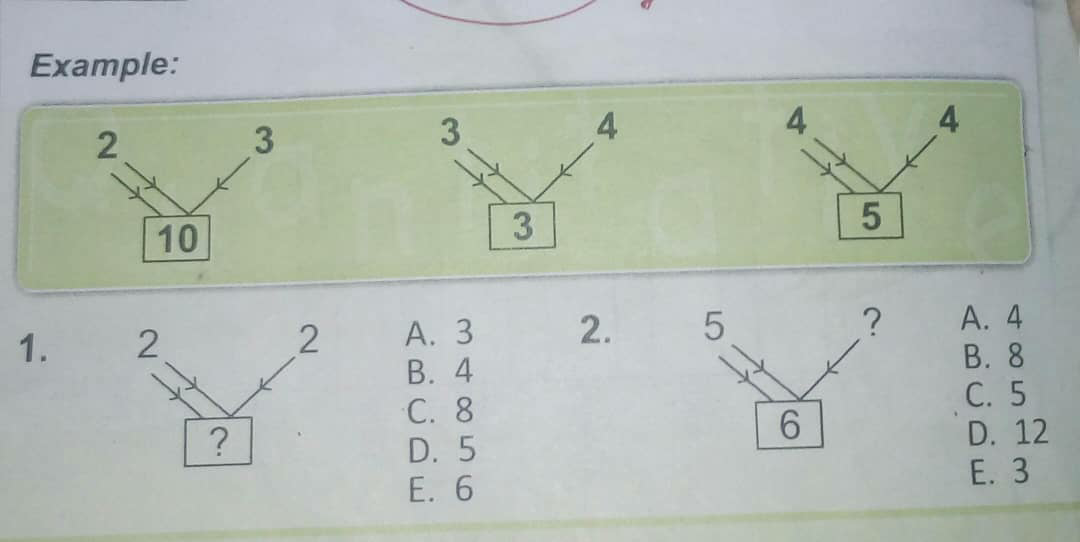
Question Number 63565 Answers: 0 Comments: 0
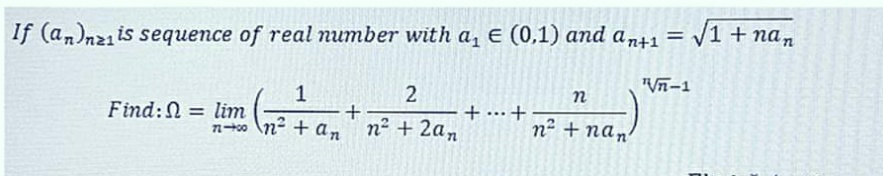
Question Number 63522 Answers: 0 Comments: 2

Question Number 63485 Answers: 1 Comments: 0
Question Number 63474 Answers: 1 Comments: 0
Question Number 63449 Answers: 0 Comments: 2
Question Number 63614 Answers: 0 Comments: 0
Question Number 63383 Answers: 1 Comments: 1
Question Number 63381 Answers: 0 Comments: 2
Question Number 63373 Answers: 0 Comments: 2
Question Number 63247 Answers: 0 Comments: 1
Pg 302 Pg 303 Pg 304 Pg 305 Pg 306 Pg 307 Pg 308 Pg 309 Pg 310 Pg 311
