
AlgebraQuestion and Answers: Page 303
Question Number 69296 Answers: 0 Comments: 6

Question Number 69276 Answers: 0 Comments: 3
Question Number 69230 Answers: 0 Comments: 0

Question Number 69226 Answers: 0 Comments: 0

Question Number 69222 Answers: 0 Comments: 1

Question Number 69201 Answers: 2 Comments: 0

Question Number 69162 Answers: 1 Comments: 0
Question Number 69143 Answers: 0 Comments: 0
Question Number 69176 Answers: 0 Comments: 1
Question Number 69072 Answers: 0 Comments: 0

Question Number 69064 Answers: 1 Comments: 3

Question Number 69020 Answers: 0 Comments: 1
Question Number 68960 Answers: 0 Comments: 3

Question Number 68935 Answers: 2 Comments: 0
Question Number 68912 Answers: 1 Comments: 0

Question Number 68899 Answers: 0 Comments: 9
Question Number 68898 Answers: 0 Comments: 7
Question Number 68835 Answers: 1 Comments: 4
Question Number 68768 Answers: 1 Comments: 1
Question Number 68740 Answers: 1 Comments: 1
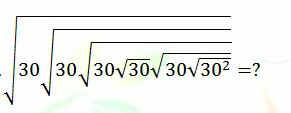
Question Number 68721 Answers: 1 Comments: 1

Question Number 68636 Answers: 2 Comments: 0
Question Number 68624 Answers: 2 Comments: 0

Question Number 68549 Answers: 1 Comments: 3
$${y}=\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}^{−\mathrm{1}} =... \\ $$
Question Number 68433 Answers: 0 Comments: 0
Question Number 68422 Answers: 1 Comments: 0

Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303 Pg 304 Pg 305 Pg 306 Pg 307
