
AlgebraQuestion and Answers: Page 302
Question Number 70617 Answers: 1 Comments: 0
Question Number 70598 Answers: 1 Comments: 0
Question Number 70518 Answers: 2 Comments: 2
Question Number 70512 Answers: 1 Comments: 1
Question Number 70460 Answers: 0 Comments: 2

Question Number 70312 Answers: 1 Comments: 1
Question Number 70216 Answers: 0 Comments: 0
Question Number 70162 Answers: 1 Comments: 0

Question Number 70161 Answers: 1 Comments: 0

Question Number 70135 Answers: 0 Comments: 1
Question Number 70103 Answers: 2 Comments: 0
Question Number 70040 Answers: 1 Comments: 3
Question Number 69995 Answers: 4 Comments: 0
Question Number 69939 Answers: 2 Comments: 12
Question Number 69741 Answers: 2 Comments: 4
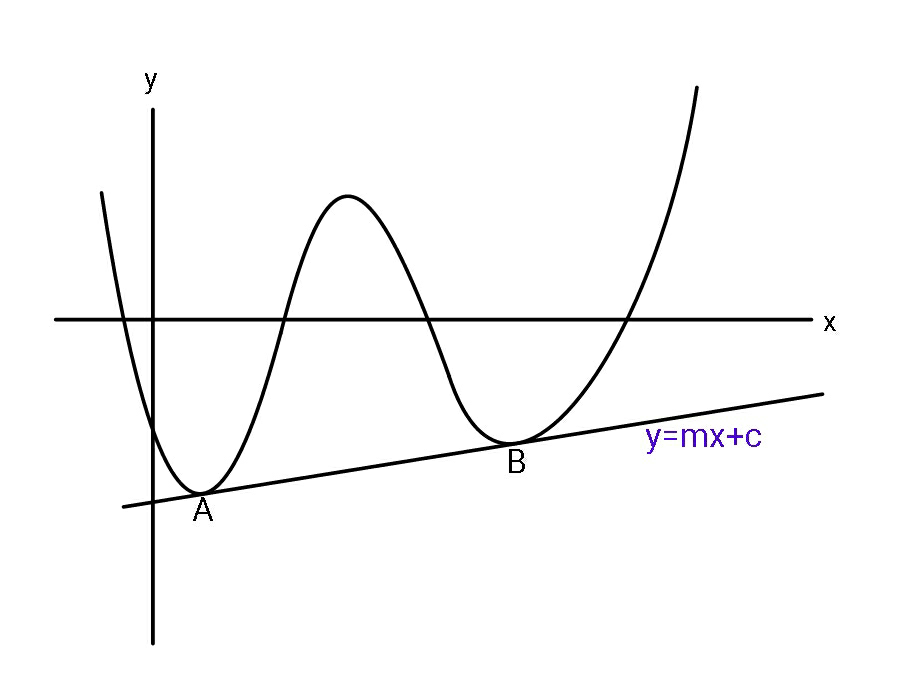
Question Number 69738 Answers: 1 Comments: 0
Question Number 71696 Answers: 1 Comments: 0
Question Number 69681 Answers: 2 Comments: 2

Question Number 69665 Answers: 1 Comments: 1

Question Number 69662 Answers: 1 Comments: 0
Question Number 69645 Answers: 1 Comments: 0
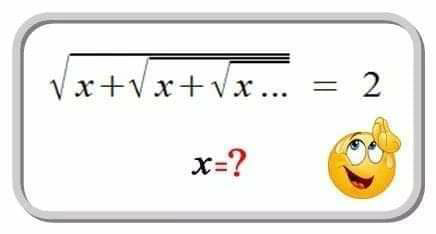
Question Number 69644 Answers: 2 Comments: 0

Question Number 69594 Answers: 1 Comments: 0

Question Number 69610 Answers: 0 Comments: 0

Question Number 69538 Answers: 0 Comments: 0
Question Number 69586 Answers: 0 Comments: 0
Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303 Pg 304 Pg 305 Pg 306
