
AlgebraQuestion and Answers: Page 300
Question Number 71729 Answers: 1 Comments: 2
$${find}\:{dU}\:\:\:{if}\:\:\:{U}={x}^{\mathrm{2}} {e}^{\frac{{x}}{{y}}} \\ $$$$ \\ $$
Question Number 71756 Answers: 1 Comments: 0
Question Number 71674 Answers: 1 Comments: 0

Question Number 71666 Answers: 1 Comments: 1
Question Number 71633 Answers: 1 Comments: 0
Question Number 71534 Answers: 2 Comments: 0
Question Number 71533 Answers: 1 Comments: 0
Question Number 71518 Answers: 1 Comments: 8
$$\mathrm{Express}\:\:\sqrt{\mathrm{28}}\:\:\mathrm{as}\:\mathrm{continued}\:\mathrm{fraction} \\ $$
Question Number 71448 Answers: 0 Comments: 1
Question Number 71406 Answers: 0 Comments: 6
Question Number 71282 Answers: 4 Comments: 0
Question Number 71242 Answers: 3 Comments: 0
Question Number 71196 Answers: 1 Comments: 0
Question Number 71172 Answers: 0 Comments: 2
Question Number 71147 Answers: 2 Comments: 1
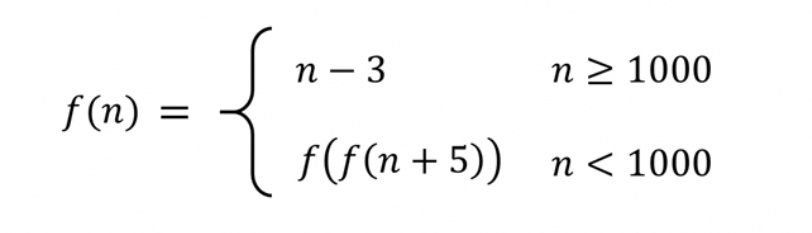
Question Number 71117 Answers: 0 Comments: 0

Question Number 71114 Answers: 0 Comments: 0

Question Number 71089 Answers: 1 Comments: 0
Question Number 71082 Answers: 2 Comments: 0
Question Number 71073 Answers: 3 Comments: 4
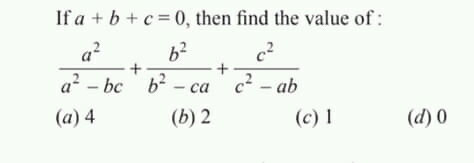
Question Number 70997 Answers: 1 Comments: 0

Question Number 70969 Answers: 1 Comments: 0

Question Number 70920 Answers: 1 Comments: 2
Question Number 70768 Answers: 1 Comments: 1

Question Number 70679 Answers: 0 Comments: 2
Question Number 70659 Answers: 1 Comments: 0
Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303 Pg 304
