Question and Answers Forum

AlgebraQuestion and Answers: Page 299

Question Number 72900 Answers: 1 Comments: 0

prove that −∣a∣≤a≤∣a∣ a is a real number

$${prove}\:{that}\: \\ $$$$ \\ $$$$−\mid{a}\mid\leqslant{a}\leqslant\mid{a}\mid \\ $$$$ \\ $$$${a}\:{is}\:{a}\:{real}\:{number} \\ $$

Question Number 72689 Answers: 1 Comments: 0

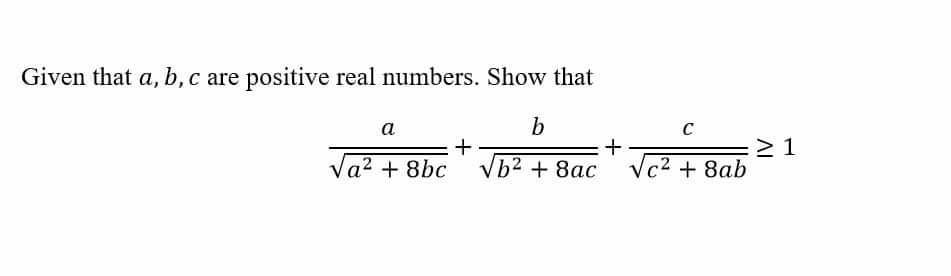
Question Number 72608 Answers: 1 Comments: 0

Question Number 72593 Answers: 2 Comments: 0

If the length of a square is increased by 25% while its width is decrease by 15% to form a rectangle. What is the ratio of the area of the rectangle to the area of the square

$$\mathrm{If}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{a}\:\mathrm{square}\:\mathrm{is}\:\mathrm{increased}\:\mathrm{by}\:\:\mathrm{25\%}\:\mathrm{while}\:\mathrm{its} \\ $$$$\mathrm{width}\:\mathrm{is}\:\mathrm{decrease}\:\mathrm{by}\:\:\:\mathrm{15\%}\:\:\:\mathrm{to}\:\mathrm{form}\:\mathrm{a}\:\mathrm{rectangle}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square} \\ $$

Question Number 72496 Answers: 2 Comments: 0

if a^x =b, b^y =c, c^z =a then prove that, xyz=0.

$$\mathrm{if}\:\mathrm{a}^{\mathrm{x}} =\mathrm{b},\:\mathrm{b}^{\mathrm{y}} =\mathrm{c},\:\mathrm{c}^{\mathrm{z}} =\mathrm{a}\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}, \\ $$$$\mathrm{xyz}=\mathrm{0}. \\ $$

Question Number 72488 Answers: 2 Comments: 0

{ ((4xy=1)),((4(√(1−x^2 )) ( y−(√(1−y^2 )) )=1)) :} Resolver elsistema en R

$$\begin{cases}{\mathrm{4}{xy}=\mathrm{1}}\\{\mathrm{4}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\left(\:{y}−\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:\right)=\mathrm{1}}\end{cases} \\ $$$$ \\ $$$${Resolver}\:{elsistema}\:{en}\:{R} \\ $$

Question Number 72483 Answers: 2 Comments: 0

Σ_(k = 0) ^n cos(a + kb)

$$\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\:\mathrm{cos}\left(\mathrm{a}\:+\:\mathrm{kb}\right) \\ $$

Question Number 72443 Answers: 1 Comments: 0

2[0.5{48−31}^2 +35]=?

$$\mathrm{2}\left[\mathrm{0}.\mathrm{5}\left\{\mathrm{48}−\mathrm{31}\right\}^{\mathrm{2}} +\mathrm{35}\right]=? \\ $$

Question Number 72421 Answers: 1 Comments: 0

Question Number 72413 Answers: 0 Comments: 0

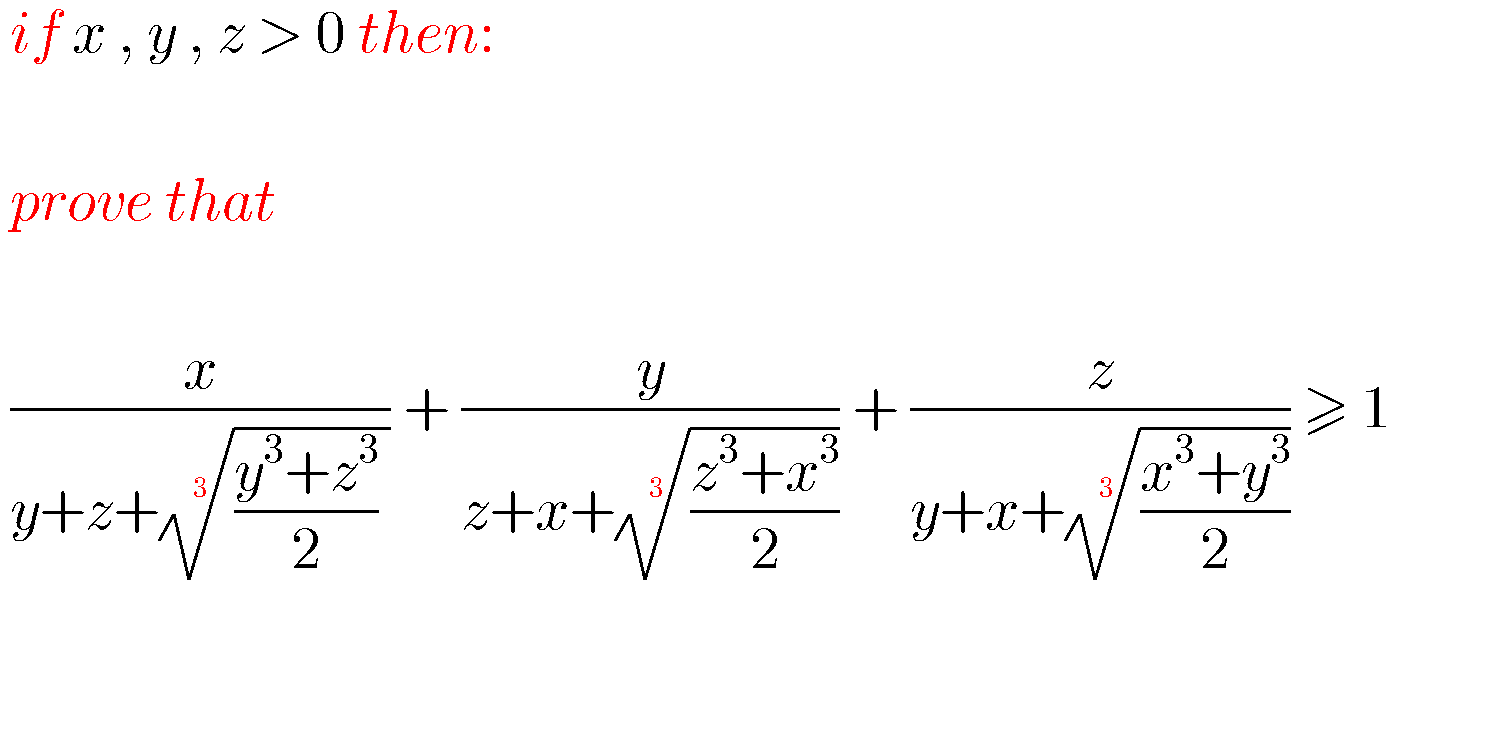
Question Number 72332 Answers: 1 Comments: 0

let Q=((1+tan(((3π)/8)) . tan((π/(10))))/(1−tan((π/8)).tan((π/(10))))) prove that ((Q−1)/(Q+1))=(√(7−3(√5)−(√(85−38(√5)))))

$${let}\:{Q}=\frac{\mathrm{1}+{tan}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:.\:{tan}\left(\frac{\pi}{\mathrm{10}}\right)}{\mathrm{1}−{tan}\left(\frac{\pi}{\mathrm{8}}\right).{tan}\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$$ \\ $$$${prove}\:{that} \\ $$$$\: \\ $$$$\frac{{Q}−\mathrm{1}}{{Q}+\mathrm{1}}=\sqrt{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}−\sqrt{\mathrm{85}−\mathrm{38}\sqrt{\mathrm{5}}}} \\ $$$$ \\ $$

Question Number 72291 Answers: 1 Comments: 0

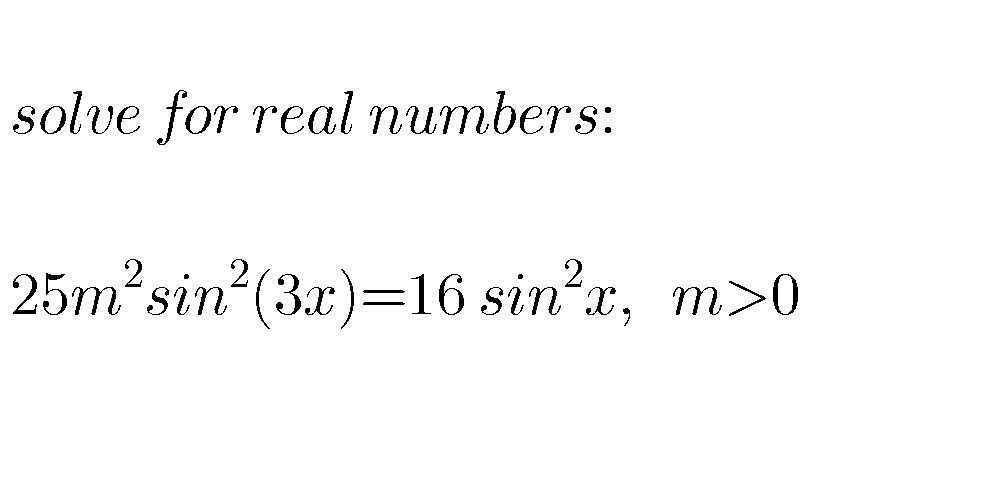
Question Number 72289 Answers: 2 Comments: 0

Bonjour. Aidez moi a resoudre le systeme suivant dans R^2 x−y=2 xy=20

$${Bonjour}. \\ $$$${Aidez}\:{moi}\:{a}\:{resoudre}\:{le}\:{systeme}\: \\ $$$${suivant}\:\:\:\:{dans}\:\mathbb{R}^{\mathrm{2}} \:\:\:\:\: \\ $$$${x}−{y}=\mathrm{2} \\ $$$${xy}=\mathrm{20} \\ $$

Question Number 72190 Answers: 1 Comments: 2

3^x +4^x =5^x

$$\mathrm{3}^{\mathrm{x}} +\mathrm{4}^{\mathrm{x}} =\mathrm{5}^{\mathrm{x}} \\ $$

Question Number 72185 Answers: 0 Comments: 2

Question Number 72118 Answers: 0 Comments: 1

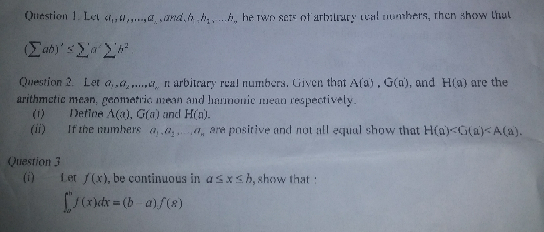
Question Number 72117 Answers: 0 Comments: 1

Please help with the proof of cauchy inequality.

$${Please}\:{help}\:{with}\:{the}\:{proof}\:{of}\:{cauchy}\:{inequality}. \\ $$

Question Number 72112 Answers: 1 Comments: 0

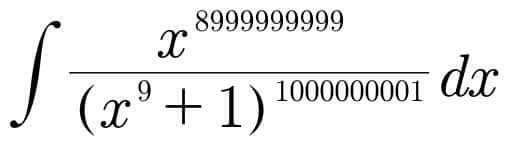
Question Number 72111 Answers: 0 Comments: 1

Question Number 72175 Answers: 1 Comments: 3

(x^2 +y^2 −1)^3 =x^2 y^3 how large (area) is your heart ♥ ?

$$\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} =\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{3}} \\ $$$$ \\ $$$${how}\:{large}\:\left({area}\right)\:{is}\:{your}\:{heart}\:\heartsuit\:? \\ $$

Question Number 74587 Answers: 0 Comments: 0

If sum of n arithmetic means between two number is 20.if last mean is double of 1st mean and one is three times of another number. find the numbers.

$$\mathrm{If}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{n}\:\mathrm{arithmetic}\:\mathrm{means}\:\mathrm{between}\: \\ $$$$\mathrm{two}\:\mathrm{number}\:\mathrm{is}\:\mathrm{20}.\mathrm{if}\:\mathrm{last}\:\mathrm{mean}\:\mathrm{is}\:\mathrm{double} \\ $$$$\mathrm{of}\:\mathrm{1st}\:\mathrm{mean}\:\mathrm{and}\:\mathrm{one}\:\mathrm{is}\:\mathrm{three}\:\mathrm{times}\:\mathrm{of} \\ $$$$\mathrm{another}\:\mathrm{number}.\:\mathrm{find}\:\mathrm{the}\:\mathrm{numbers}. \\ $$$$ \\ $$

Question Number 71960 Answers: 1 Comments: 0

Question Number 71946 Answers: 1 Comments: 0

Question Number 71926 Answers: 1 Comments: 2

Question Number 71824 Answers: 2 Comments: 1

solve x^x^x^(2019) =2019

$${solve}\: \\ $$$${x}^{{x}^{{x}^{\mathrm{2019}} } } =\mathrm{2019} \\ $$

Question Number 71810 Answers: 0 Comments: 0

Pg 294 Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303

Contact: info@tinkutara.com