Question and Answers Forum

All Questions Topic List

AlgebraQuestion and Answers: Page 295

Question Number 76048 Answers: 2 Comments: 0

∫e^x^2 dx

$$\int{e}^{{x}^{\mathrm{2}} } {dx} \\ $$

Question Number 76009 Answers: 1 Comments: 0

hiw do i solve 2^x = 4x?

$${hiw}\:{do}\:{i}\:{solve} \\ $$$$\mathrm{2}^{{x}} \:=\:\mathrm{4}{x}? \\ $$

Question Number 76003 Answers: 1 Comments: 0

22+2

$$\mathrm{22}+\mathrm{2} \\ $$

Question Number 75990 Answers: 0 Comments: 0

Question Number 75985 Answers: 1 Comments: 0

Question Number 75933 Answers: 0 Comments: 2

solve the inequality a. ln(2x−e) >1 b. (lnx)^2 −lnx−6<0 c. ∣x∣ + ∣x+2∣ ≥ 2 d. ∣2x−5∣ + ∣x +2∣ > 7

$${solve}\:{the}\:{inequality} \\ $$$${a}.\:\:{ln}\left(\mathrm{2}{x}−{e}\right)\:>\mathrm{1} \\ $$$${b}.\:\left({lnx}\right)^{\mathrm{2}} −{lnx}−\mathrm{6}<\mathrm{0} \\ $$$${c}.\:\mid{x}\mid\:+\:\mid{x}+\mathrm{2}\mid\:\geqslant\:\mathrm{2} \\ $$$${d}.\:\mid\mathrm{2}{x}−\mathrm{5}\mid\:+\:\mid{x}\:+\mathrm{2}\mid\:>\:\mathrm{7} \\ $$

Question Number 75932 Answers: 1 Comments: 1

solve for x the following a. ∣x∣ + 3x −4 =0 b. ∣x∣−1 = 0 c. x^2 +3∣x∣ +2 =0

$${solve}\:{for}\:{x}\:{the}\:{following} \\ $$$${a}.\:\mid{x}\mid\:+\:\mathrm{3}{x}\:−\mathrm{4}\:=\mathrm{0} \\ $$$${b}.\:\:\mid{x}\mid−\mathrm{1}\:=\:\mathrm{0} \\ $$$${c}.\:{x}^{\mathrm{2}} +\mathrm{3}\mid{x}\mid\:+\mathrm{2}\:=\mathrm{0} \\ $$$$ \\ $$

Question Number 75916 Answers: 0 Comments: 1

x^3 +x^2 −24x+36=0 prove that x=2,3,−6.

$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{24}{x}+\mathrm{36}=\mathrm{0} \\ $$$${prove}\:{that}\:{x}=\mathrm{2},\mathrm{3},−\mathrm{6}. \\ $$

Question Number 75913 Answers: 0 Comments: 1

x^3 −7x+6=0 prove that x=2,−3,1 .

$${x}^{\mathrm{3}} −\mathrm{7}{x}+\mathrm{6}=\mathrm{0} \\ $$$${prove}\:{that}\:{x}=\mathrm{2},−\mathrm{3},\mathrm{1}\:. \\ $$

Question Number 75918 Answers: 1 Comments: 0

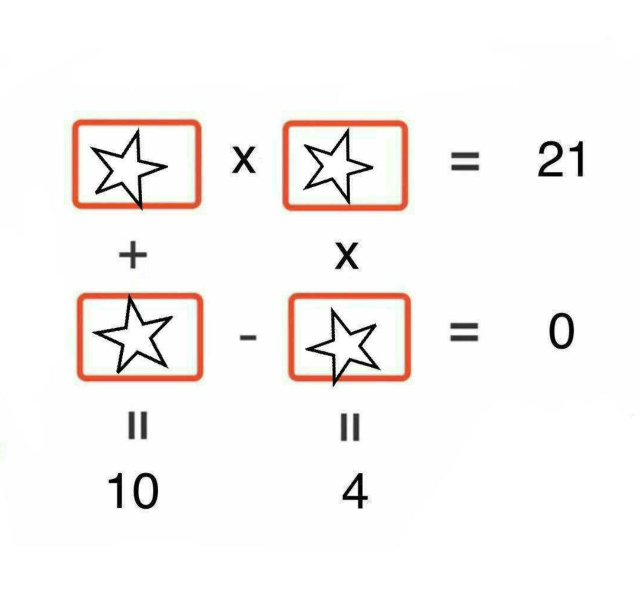
Question Number 75883 Answers: 0 Comments: 2

If a^4 + b^4 + c^4 + d^4 = 16 Prove that, a^5 + b^5 + c^5 + d^5 ≤ 32

$$\mathrm{If}\:\:\:\:\mathrm{a}^{\mathrm{4}} \:+\:\mathrm{b}^{\mathrm{4}} \:+\:\mathrm{c}^{\mathrm{4}} \:+\:\mathrm{d}^{\mathrm{4}} \:\:\:=\:\:\:\mathrm{16} \\ $$$$\mathrm{Prove}\:\mathrm{that},\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{5}} \:+\:\mathrm{b}^{\mathrm{5}} \:+\:\mathrm{c}^{\mathrm{5}} \:+\:\mathrm{d}^{\mathrm{5}} \:\:\:\leqslant\:\:\:\mathrm{32} \\ $$

Question Number 75845 Answers: 1 Comments: 2

{ ((x+yz=x^2 )),((y+xz=y^2 )),((z+xy=z^2 )) :} solve for x,y,z.

$$\begin{cases}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{yz}}=\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\\{\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{xz}}=\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\\{\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{xy}}=\boldsymbol{\mathrm{z}}^{\mathrm{2}} }\end{cases}\:\:\:\:\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}}. \\ $$

Question Number 75828 Answers: 1 Comments: 1

Σ_(n=1) ^∞ (1/(10^n ))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{10}^{{n}} } \\ $$

Question Number 75846 Answers: 2 Comments: 0

sin^5 x+(√2)sinx=1 , x∈[0,2𝛑]

$$\boldsymbol{\mathrm{sin}}^{\mathrm{5}} \boldsymbol{\mathrm{x}}+\sqrt{\mathrm{2}}\boldsymbol{\mathrm{sinx}}=\mathrm{1}\:\:\:\:\:\:\:\:,\:\:\boldsymbol{\mathrm{x}}\in\left[\mathrm{0},\mathrm{2}\boldsymbol{\pi}\right] \\ $$

Question Number 75778 Answers: 1 Comments: 0

if x^2 +y^2 =p, x^3 +y^3 =q, find x^n +y^n in terms of p, q and n. (n≥4)

$${if}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={p},\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} ={q}, \\ $$$${find}\:{x}^{{n}} +{y}^{{n}} \:{in}\:{terms}\:{of}\:{p},\:{q}\:{and}\:{n}. \\ $$$$\left({n}\geqslant\mathrm{4}\right) \\ $$

Question Number 75756 Answers: 0 Comments: 1

Σ_(x=1) ^(99) ((1/(2x+1)))

$$\underset{{x}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}\right) \\ $$

Question Number 75753 Answers: 1 Comments: 0

((((x^(1/3) +x^(−1/3) )^2 −2)/((x^(1/3) +x^(−1/3) )^2 +2))−x)^(3/4)

$$\left(\frac{\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{x}^{−\mathrm{1}/\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{2}}{\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{x}^{−\mathrm{1}/\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{2}}−\mathrm{x}\right)^{\mathrm{3}/\mathrm{4}} \\ $$

Question Number 75751 Answers: 0 Comments: 0

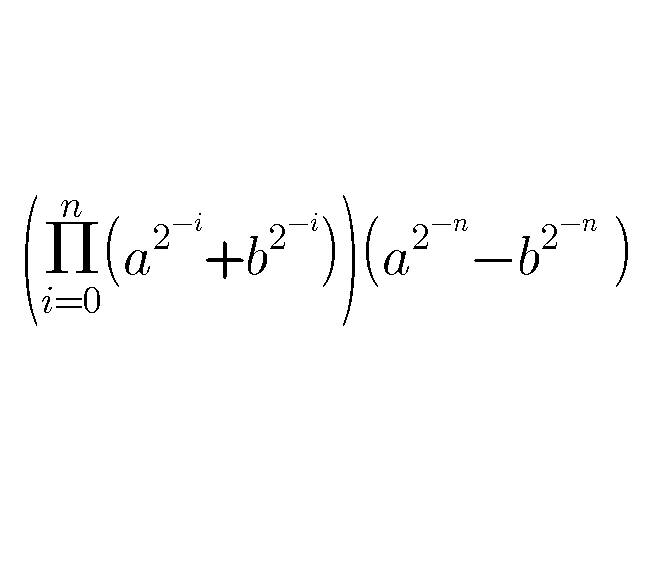
Question Number 75739 Answers: 1 Comments: 1

Question Number 75681 Answers: 1 Comments: 8

Question Number 75669 Answers: 3 Comments: 3

Question Number 75661 Answers: 1 Comments: 0

Question Number 75660 Answers: 2 Comments: 1

find all solutions (if exist) of x^2 +5y^2 =2016 with x,y ∈ N.

$${find}\:{all}\:{solutions}\:\left({if}\:{exist}\right)\:{of} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{y}^{\mathrm{2}} =\mathrm{2016} \\ $$$${with}\:{x},{y}\:\in\:\mathbb{N}. \\ $$

Question Number 75655 Answers: 1 Comments: 0

if z ∈ C is sin^2 z+cos^2 z=1 also valid?

$${if}\:{z}\:\in\:\mathbb{C} \\ $$$${is}\:\mathrm{sin}^{\mathrm{2}} \:{z}+\mathrm{cos}^{\mathrm{2}} \:{z}=\mathrm{1}\:{also}\:{valid}? \\ $$

Question Number 75618 Answers: 0 Comments: 3

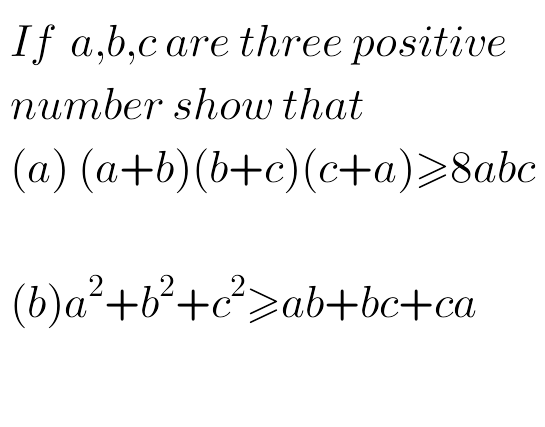
Question Number 75616 Answers: 1 Comments: 7

A_1 =2 B_1 =1 A_(n+1) =A_n −8B_n B_(n+1) =A_n +7B_n find A_n =?, B_n =?

$${A}_{\mathrm{1}} =\mathrm{2} \\ $$$${B}_{\mathrm{1}} =\mathrm{1} \\ $$$${A}_{{n}+\mathrm{1}} ={A}_{{n}} −\mathrm{8}{B}_{{n}} \\ $$$${B}_{{n}+\mathrm{1}} ={A}_{{n}} +\mathrm{7}{B}_{{n}} \\ $$$${find}\:{A}_{{n}} =?,\:{B}_{{n}} =? \\ $$

Pg 290 Pg 291 Pg 292 Pg 293 Pg 294 Pg 295 Pg 296 Pg 297 Pg 298 Pg 299

Contact: info@tinkutara.com