
AlgebraQuestion and Answers: Page 289
Question Number 80084 Answers: 0 Comments: 3
Question Number 80068 Answers: 2 Comments: 3

Question Number 80053 Answers: 0 Comments: 4
Question Number 80108 Answers: 1 Comments: 3
Question Number 80039 Answers: 1 Comments: 6
Question Number 79998 Answers: 0 Comments: 3
Question Number 79978 Answers: 3 Comments: 0
Question Number 79974 Answers: 1 Comments: 0

Question Number 80004 Answers: 1 Comments: 2
Question Number 79932 Answers: 1 Comments: 1

Question Number 79883 Answers: 0 Comments: 9
Question Number 79876 Answers: 1 Comments: 1
Question Number 79947 Answers: 0 Comments: 4
Question Number 79946 Answers: 2 Comments: 0
Question Number 79864 Answers: 0 Comments: 0

Question Number 79861 Answers: 0 Comments: 1

Question Number 79826 Answers: 0 Comments: 7
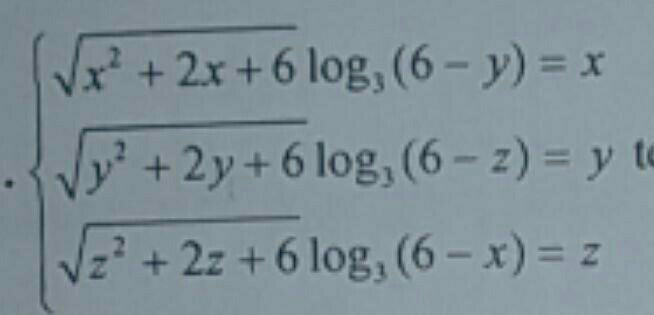
Question Number 79807 Answers: 2 Comments: 2

Question Number 79792 Answers: 1 Comments: 1
Question Number 79757 Answers: 0 Comments: 1
Question Number 79635 Answers: 0 Comments: 9
Question Number 79571 Answers: 1 Comments: 5
Question Number 79613 Answers: 1 Comments: 0
Question Number 79560 Answers: 0 Comments: 1
$$\sqrt{\mathrm{1}+\mathrm{x}}\:\leqslant\:\sqrt[{\mathrm{4}\:}]{\mathrm{5}−\mathrm{x}} \\ $$
Question Number 79538 Answers: 1 Comments: 13
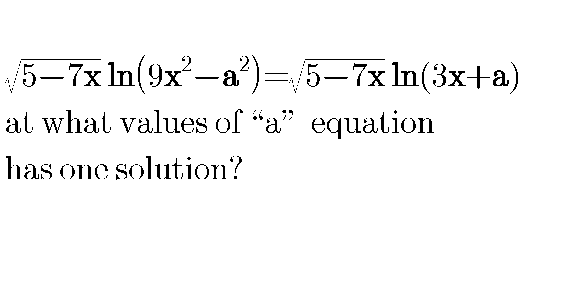
Question Number 79536 Answers: 0 Comments: 4

Pg 284 Pg 285 Pg 286 Pg 287 Pg 288 Pg 289 Pg 290 Pg 291 Pg 292 Pg 293
