Question and Answers Forum

AlgebraQuestion and Answers: Page 287

Question Number 80362 Answers: 1 Comments: 0

Question Number 80306 Answers: 0 Comments: 1

Question Number 80347 Answers: 1 Comments: 6

let x and y be positif real number such that 1≤x+y≤9 and x≤2y≤3x. what is the largest value of ((9−y)/(9−x))

$${let}\:{x}\:{and}\:{y}\:{be}\:{positif}\:{real}\:{number} \\ $$$${such}\:{that}\:\mathrm{1}\leqslant{x}+{y}\leqslant\mathrm{9}\:{and} \\ $$$${x}\leqslant\mathrm{2}{y}\leqslant\mathrm{3}{x}.\:{what}\:{is}\:{the}\: \\ $$$${largest}\:{value}\:{of}\:\:\:\frac{\mathrm{9}−{y}}{\mathrm{9}−{x}} \\ $$$$ \\ $$

Question Number 80262 Answers: 0 Comments: 2

Question Number 80261 Answers: 0 Comments: 1

Question Number 80243 Answers: 0 Comments: 7

if x+(1/x)=a (a∈R) find x^n +(1/x^n )=? (n∈N)

$${if}\:{x}+\frac{\mathrm{1}}{{x}}={a}\:\left({a}\in\mathbb{R}\right) \\ $$$${find}\:{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=? \\ $$$$\left({n}\in\mathbb{N}\right) \\ $$

Question Number 80219 Answers: 1 Comments: 0

Question Number 80209 Answers: 2 Comments: 1

Question Number 80208 Answers: 0 Comments: 0

Question Number 80204 Answers: 0 Comments: 2

Question Number 80199 Answers: 2 Comments: 1

Question Number 80178 Answers: 0 Comments: 4

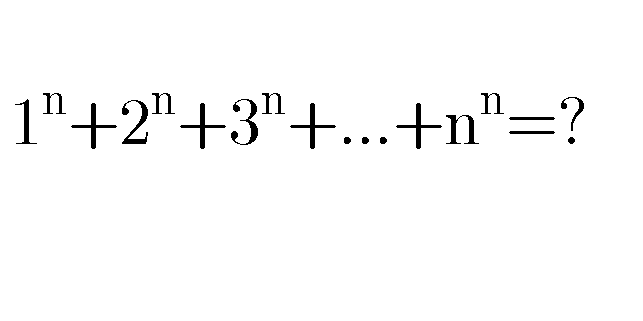
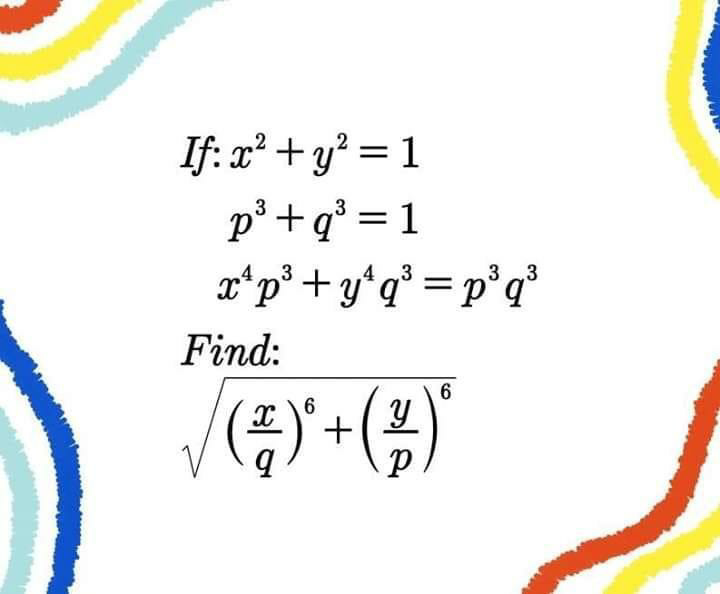
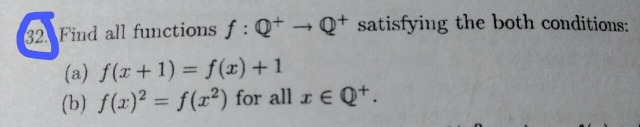
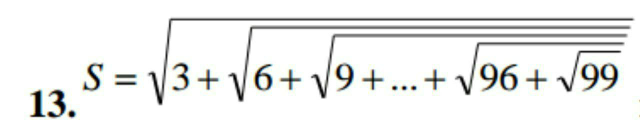
Question Number 80161 Answers: 0 Comments: 10

Find the relation between q and r so that x^3 +3px^2 +qx+r is a perfect cube for all value of x

$${Find}\:{the}\:{relation}\:{between} \\ $$$${q}\:{and}\:{r}\:\:{so}\:\:{that} \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{px}^{\mathrm{2}} +{qx}+{r}\:{is}\:{a}\:{perfect} \\ $$$${cube}\:{for}\:{all}\:\:{value}\:{of}\:{x} \\ $$

Question Number 80160 Answers: 0 Comments: 1

∫_0 ^∞ (x^3 /(e^(2x) −e^x ))

$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} }{{e}^{\mathrm{2}{x}} −{e}^{{x}} } \\ $$

Question Number 80139 Answers: 1 Comments: 6

Question Number 80142 Answers: 2 Comments: 0

a. Σ_(k=1) ^∞ ((k^3 /2^k ))=? b. Σ_(k=1) ^∞ (((k^3 +k^2 +k+1)/7^k ))=?

$$\mathrm{a}.\:\:\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\boldsymbol{\mathrm{k}}^{\mathrm{3}} }{\mathrm{2}^{\boldsymbol{\mathrm{k}}} }\right)=? \\ $$$$\boldsymbol{\mathrm{b}}.\:\:\:\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\boldsymbol{\mathrm{k}}^{\mathrm{3}} +\boldsymbol{\mathrm{k}}^{\mathrm{2}} +\boldsymbol{\mathrm{k}}+\mathrm{1}}{\mathrm{7}^{\boldsymbol{\mathrm{k}}} }\right)=? \\ $$

Question Number 80131 Answers: 0 Comments: 2

Question Number 80145 Answers: 1 Comments: 5

{ (((x/a)+(y/b)=a^2 +b^2 )),(( [a,b∈R])),((ab(x^2 −y^2 )=xy(a^2 −b^2 ))) :}

$$\begin{cases}{\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{a}}}+\frac{\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{b}}}=\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} }\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\in\boldsymbol{\mathrm{R}}\right]}\\{\boldsymbol{\mathrm{ab}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{y}}^{\mathrm{2}} \right)=\boldsymbol{\mathrm{xy}}\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)}\end{cases} \\ $$

Question Number 80144 Answers: 0 Comments: 1

solve for x: (((√x)+1)/(√(x+1)))+ax^2 =x(a^2 +1) [a∈R]

$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{x}}: \\ $$$$\frac{\sqrt{\boldsymbol{\mathrm{x}}}+\mathrm{1}}{\sqrt{\boldsymbol{\mathrm{x}}+\mathrm{1}}}+\boldsymbol{\mathrm{ax}}^{\mathrm{2}} =\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{1}\right)\:\:\:\:\:\:\left[\boldsymbol{\mathrm{a}}\in\boldsymbol{\mathrm{R}}\right] \\ $$

Question Number 80116 Answers: 1 Comments: 1

Find S_m =Σ_(n=0) ^∞ (1/(Π_(k=1) ^m (n+k)))=? (m≥2)

$${Find} \\ $$$${S}_{{m}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left({n}+{k}\right)}=? \\ $$$$\left({m}\geqslant\mathrm{2}\right) \\ $$

Question Number 80093 Answers: 3 Comments: 0

Solve for x and y x^(√y) = 64 y^(√x) = 81

$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$$$\:\:\:\:\:\mathrm{x}^{\sqrt{\mathrm{y}}} \:\:\:=\:\:\mathrm{64} \\ $$$$\:\:\:\:\:\mathrm{y}^{\sqrt{\mathrm{x}}} \:\:\:=\:\mathrm{81} \\ $$

Question Number 80084 Answers: 0 Comments: 3

−1=(−1)^1 =(−1)^(2/2) =((−1)^2 )^(1/2) =(1)^(1/2) = =(√1)=1 what do you think about this?

$$\:\:−\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{1}} =\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{2}}} =\left(\left(−\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} = \\ $$$$=\sqrt{\mathrm{1}}=\mathrm{1}\:\: \\ $$$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{about}\:\mathrm{this}? \\ $$

Question Number 80068 Answers: 2 Comments: 3

Question Number 80053 Answers: 0 Comments: 4

Find integer x, y such that 2^x −y^2 =615

$${Find}\:{integer}\:{x},\:{y}\:{such}\:{that} \\ $$$$\mathrm{2}^{{x}} −{y}^{\mathrm{2}} =\mathrm{615} \\ $$

Question Number 80108 Answers: 1 Comments: 3

a,b,c ∈R ((b+c+d)/a)=((a+c+d)/b)=((a+b+c)/d)=((a+b+d)/c)=r what is r?

$${a},{b},{c}\:\in\mathbb{R} \\ $$$$\frac{{b}+{c}+{d}}{{a}}=\frac{{a}+{c}+{d}}{{b}}=\frac{{a}+{b}+{c}}{{d}}=\frac{{a}+{b}+{d}}{{c}}={r} \\ $$$${what}\:{is}\:{r}? \\ $$

Question Number 80039 Answers: 1 Comments: 6

prove that (1+x)(1+(1/x))≥4

$${prove}\:{that} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\geqslant\mathrm{4} \\ $$

Pg 282 Pg 283 Pg 284 Pg 285 Pg 286 Pg 287 Pg 288 Pg 289 Pg 290 Pg 291

Contact: info@tinkutara.com