
AlgebraQuestion and Answers: Page 274
Question Number 90747 Answers: 1 Comments: 0
Question Number 90716 Answers: 0 Comments: 1
Question Number 90661 Answers: 2 Comments: 0
Question Number 90557 Answers: 0 Comments: 7
Question Number 90550 Answers: 0 Comments: 3
Question Number 90483 Answers: 0 Comments: 0
Question Number 90473 Answers: 1 Comments: 2

Question Number 90406 Answers: 2 Comments: 0
Question Number 90379 Answers: 0 Comments: 2
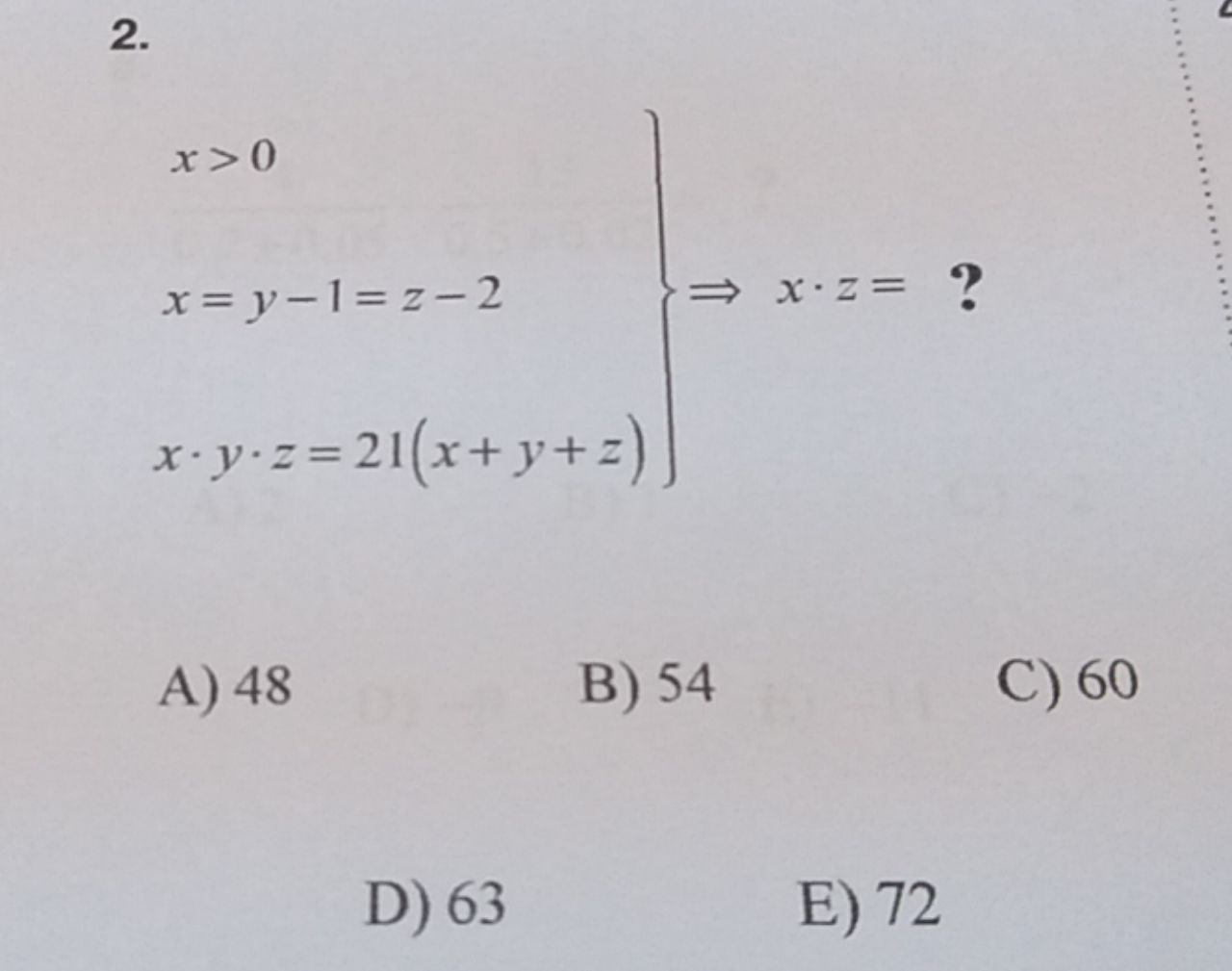
Question Number 90360 Answers: 1 Comments: 1
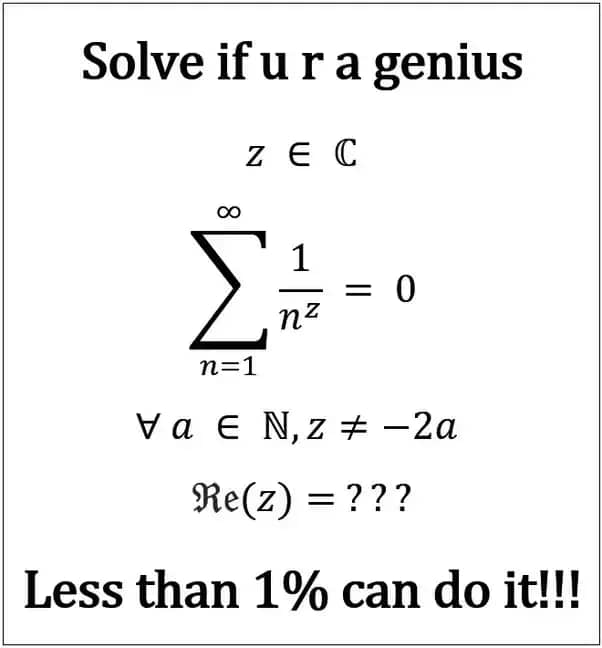
Question Number 90350 Answers: 1 Comments: 0
Question Number 90318 Answers: 0 Comments: 0
Question Number 90251 Answers: 1 Comments: 2
Question Number 90240 Answers: 0 Comments: 0
Question Number 90225 Answers: 0 Comments: 3
Question Number 90212 Answers: 0 Comments: 4
Question Number 90195 Answers: 0 Comments: 0

Question Number 90194 Answers: 1 Comments: 0
Question Number 90178 Answers: 1 Comments: 1

Question Number 90139 Answers: 0 Comments: 3
Question Number 90162 Answers: 1 Comments: 0

Question Number 90160 Answers: 1 Comments: 0
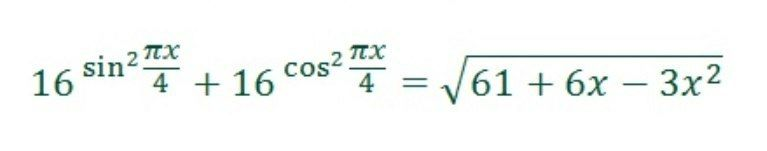
Question Number 90103 Answers: 0 Comments: 1

Question Number 90097 Answers: 0 Comments: 1
Question Number 90086 Answers: 0 Comments: 7

Question Number 90092 Answers: 0 Comments: 1
Pg 269 Pg 270 Pg 271 Pg 272 Pg 273 Pg 274 Pg 275 Pg 276 Pg 277 Pg 278
