
AlgebraQuestion and Answers: Page 271
Question Number 93129 Answers: 1 Comments: 2
$${derive}\:{x}^{\mathrm{2}} −\left(\alpha+\beta\right){x}+\alpha\beta \\ $$
Question Number 93057 Answers: 1 Comments: 1
Question Number 93039 Answers: 0 Comments: 1
Question Number 93077 Answers: 1 Comments: 1
Question Number 92885 Answers: 0 Comments: 10
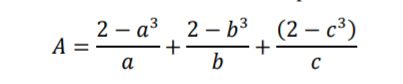
Question Number 92880 Answers: 1 Comments: 0
Question Number 92899 Answers: 0 Comments: 1
Question Number 92839 Answers: 1 Comments: 0
Question Number 92835 Answers: 0 Comments: 3

Question Number 92831 Answers: 1 Comments: 5

Question Number 92820 Answers: 1 Comments: 0
Question Number 92778 Answers: 0 Comments: 1

Question Number 92727 Answers: 1 Comments: 0
Question Number 92717 Answers: 2 Comments: 5

Question Number 92608 Answers: 0 Comments: 4

Question Number 92566 Answers: 0 Comments: 2
Question Number 92557 Answers: 0 Comments: 3
Question Number 92489 Answers: 0 Comments: 0
Question Number 92488 Answers: 0 Comments: 11
Question Number 92448 Answers: 4 Comments: 1
Question Number 92426 Answers: 0 Comments: 4
$$\mathrm{If}\:\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}=\mathrm{0}\:\mathrm{find}\:\mathrm{y} \\ $$
Question Number 92425 Answers: 0 Comments: 1
Question Number 92390 Answers: 0 Comments: 2
Question Number 92366 Answers: 0 Comments: 3

Question Number 92346 Answers: 3 Comments: 3
Question Number 92335 Answers: 0 Comments: 0
$$\sqrt{\left\{\mathrm{x}\right\}}\:=\:\mathrm{1}+\:\mathrm{ln}\left(\mathrm{x}\right)\: \\ $$
Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271 Pg 272 Pg 273 Pg 274 Pg 275
