
AlgebraQuestion and Answers: Page 268
Question Number 96072 Answers: 1 Comments: 0
Question Number 96021 Answers: 0 Comments: 1
Question Number 95964 Answers: 0 Comments: 0
Question Number 95967 Answers: 1 Comments: 1

Question Number 95920 Answers: 3 Comments: 0
Question Number 95919 Answers: 1 Comments: 0
Question Number 95898 Answers: 0 Comments: 0
Question Number 95843 Answers: 1 Comments: 0
Question Number 95789 Answers: 1 Comments: 1
Question Number 95767 Answers: 1 Comments: 0

Question Number 95766 Answers: 0 Comments: 1
Question Number 95765 Answers: 0 Comments: 3
Question Number 95742 Answers: 2 Comments: 2
Question Number 95668 Answers: 1 Comments: 2
Question Number 95648 Answers: 0 Comments: 8
Question Number 95608 Answers: 3 Comments: 2
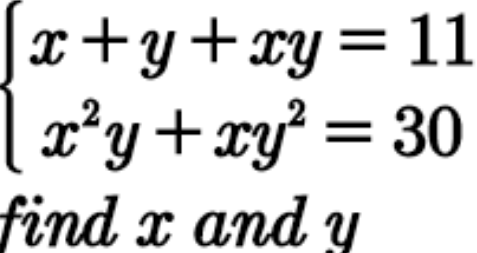
Question Number 95560 Answers: 1 Comments: 1

Question Number 95502 Answers: 1 Comments: 3
Question Number 95469 Answers: 0 Comments: 1
Question Number 95447 Answers: 1 Comments: 0
Question Number 95440 Answers: 1 Comments: 0
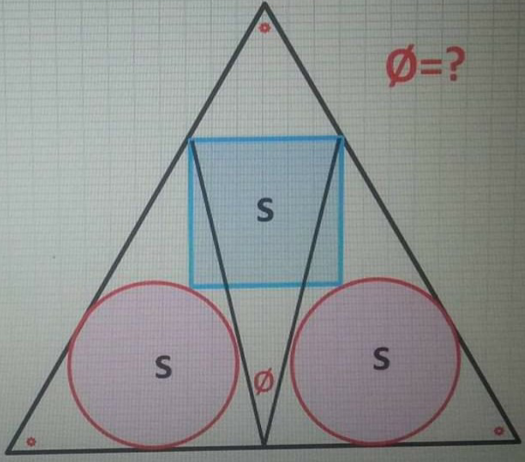
Question Number 95416 Answers: 1 Comments: 4
Question Number 95394 Answers: 0 Comments: 31
Question Number 95373 Answers: 1 Comments: 2
Question Number 95328 Answers: 0 Comments: 3

Question Number 95324 Answers: 0 Comments: 2
Pg 263 Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271 Pg 272
