Question and Answers Forum

AlgebraQuestion and Answers: Page 267

Question Number 97019 Answers: 0 Comments: 1

Question Number 96951 Answers: 1 Comments: 5

prove that 1−(1/2)+(1/3)−(1/4)+(1/5)+...+((−1^(n−1) )/n) is always positive

$${prove}\:{that}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+...+\frac{−\mathrm{1}^{{n}−\mathrm{1}} }{{n}}\:\:{is}\:{always}\:{positive} \\ $$$$ \\ $$

Question Number 96868 Answers: 0 Comments: 1

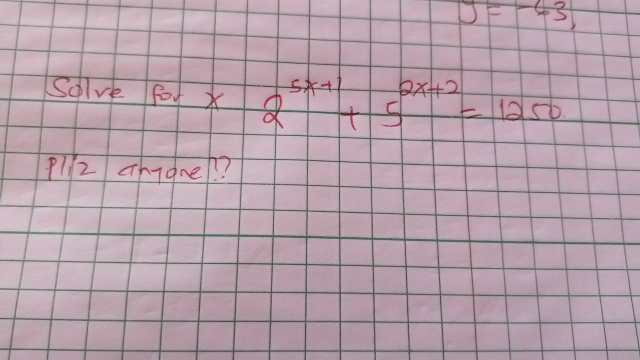
Question Number 96839 Answers: 0 Comments: 0

Question Number 96829 Answers: 0 Comments: 1

If 2f(x) + f(1−x) = x^2 . determine f(x)

$$\mathrm{If}\:\mathrm{2f}\left(\mathrm{x}\right)\:+\:\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} .\:\mathrm{determine}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$

Question Number 96821 Answers: 3 Comments: 0

{ (((u^2 /v) + (v^2 /u) = 12)),(((1/u) + (1/v) = (1/3))) :} . find u and v ?

$$\begin{cases}{\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{v}}\:+\:\frac{\mathrm{v}^{\mathrm{2}} }{\mathrm{u}}\:=\:\mathrm{12}}\\{\frac{\mathrm{1}}{\mathrm{u}}\:+\:\frac{\mathrm{1}}{\mathrm{v}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}}\end{cases}\:.\:\mathrm{find}\:\mathrm{u}\:\mathrm{and}\:\mathrm{v}\:? \\ $$

Question Number 96749 Answers: 1 Comments: 0

how we can calclate triple factorial?

$$\mathrm{how}\:\mathrm{we}\:\mathrm{can}\:\mathrm{calclate}\:\mathrm{triple}\:\mathrm{factorial}? \\ $$

Question Number 96715 Answers: 1 Comments: 0

find real solution of equation x^5 +x^4 +1 = 0

$$\mathrm{find}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{equation} \\ $$$${x}^{\mathrm{5}} +{x}^{\mathrm{4}} +\mathrm{1}\:=\:\mathrm{0} \\ $$

Question Number 96712 Answers: 1 Comments: 0

Question Number 96650 Answers: 1 Comments: 0

solve 2 ((2y−1))^(1/(3 )) = y^3 +1

$$\mathrm{solve}\:\mathrm{2}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2y}−\mathrm{1}}\:=\:\mathrm{y}^{\mathrm{3}} +\mathrm{1} \\ $$

Question Number 96584 Answers: 1 Comments: 4

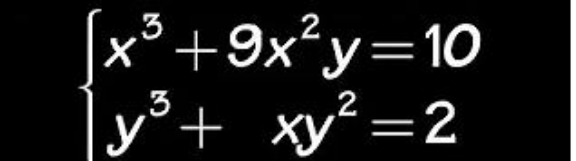
Question Number 96527 Answers: 2 Comments: 1

proof that 1^2 +2^2 +3^2 +....+n^2 =((n(2n+1)(n+1))/6)

$$\mathrm{proof}\:\mathrm{that}\:\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +....+\mathrm{n}^{\mathrm{2}} =\frac{\mathrm{n}\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$

Question Number 96505 Answers: 2 Comments: 2

((√((8)^(1/(4 )) −(√((√2)+1))))/((√((8)^(1/(4 )) +(√((√2)−1))))−(√((8)^(1/(4 )) −(√((√2)−1)))))) ?

$$\frac{\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}}}{\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}−\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}}\:? \\ $$

Question Number 96460 Answers: 1 Comments: 8

Question Number 96407 Answers: 1 Comments: 4

Question Number 96390 Answers: 1 Comments: 0

Question Number 96340 Answers: 0 Comments: 4

The equations of two circles S_1 and S_2 are given by S_1 : x^2 + y^2 +2x +2y + 1 = 0 S_2 : x^2 + y^2 −4x + 2y +1 = 0. Show that S_1 and S_2 touch each other externally and obtain the equation of the common tangent T at the point of contact.

$$\mathrm{The}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{two}\:\mathrm{circles}\:{S}_{\mathrm{1}} \:\mathrm{and}\:{S}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{given}\:\mathrm{by} \\ $$$$\:{S}_{\mathrm{1}} :\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{2}{y}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\:{S}_{\mathrm{2}} :\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:−\mathrm{4}{x}\:+\:\mathrm{2}{y}\:+\mathrm{1}\:=\:\mathrm{0}. \\ $$$$\mathrm{Show}\:\mathrm{that}\:{S}_{\mathrm{1}} \:\mathrm{and}\:{S}_{\mathrm{2}} \:\mathrm{touch}\:\mathrm{each}\:\mathrm{other}\:\mathrm{externally}\:\mathrm{and}\:\mathrm{obtain} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{common}\:\mathrm{tangent}\:{T}\:\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\:\mathrm{contact}. \\ $$

Question Number 96329 Answers: 0 Comments: 2

x⌊x⌊x⌊x⌋⌋⌋=88 x>0

$${x}\lfloor{x}\lfloor{x}\lfloor{x}\rfloor\rfloor\rfloor=\mathrm{88} \\ $$$${x}>\mathrm{0} \\ $$

Question Number 96321 Answers: 1 Comments: 1

It is given that x^2 =2^x . Find x.

$${It}\:{is}\:{given}\:{that}\:{x}^{\mathrm{2}} =\mathrm{2}^{{x}} .\:{Find}\:{x}. \\ $$

Question Number 96311 Answers: 1 Comments: 0

(4+(√(15)))^x + (4−(√(15)))^x = 62 x=?

$$\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} \:+\:\left(\mathrm{4}−\sqrt{\mathrm{15}}\right)^{{x}} \:=\:\mathrm{62}\: \\ $$$${x}=? \\ $$

Question Number 96296 Answers: 1 Comments: 0

Question Number 96289 Answers: 0 Comments: 1

1010^x +2020^x =4040^x x=?

$$\mathrm{1010}^{{x}} +\mathrm{2020}^{{x}} =\mathrm{4040}^{{x}} \\ $$$${x}=? \\ $$

Question Number 96244 Answers: 1 Comments: 2

The line y = mx meets the parabola y = (x − a)(b − x) tangentially where 0 < a < b. Show that m = ((√b) − (√a))^2

$$ \\ $$$$\:\:\mathrm{The}\:\mathrm{line}\:{y}\:=\:{mx}\:\:\mathrm{meets}\:\mathrm{the}\:\mathrm{parabola} \\ $$$$\:\:{y}\:=\:\left({x}\:−\:{a}\right)\left({b}\:−\:{x}\right)\:\mathrm{tangentially}\:\mathrm{where} \\ $$$$\:\:\mathrm{0}\:<\:{a}\:<\:{b}.\:\mathrm{Show}\:\mathrm{that}\:{m}\:=\:\left(\sqrt{{b}}\:−\:\sqrt{{a}}\right)^{\mathrm{2}} \\ $$$$ \\ $$

Question Number 96189 Answers: 3 Comments: 0

find a common roots from the two quadratic eq 24x^2 +(p+4)x−1=0 and 6x^2 +11x+p+2=0

$$\mathrm{find}\:\mathrm{a}\:\mathrm{common}\:\mathrm{roots}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{two}\:\mathrm{quadratic}\:\mathrm{eq} \\ $$$$\mathrm{24x}^{\mathrm{2}} +\left(\mathrm{p}+\mathrm{4}\right)\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{6x}^{\mathrm{2}} +\mathrm{11x}+\mathrm{p}+\mathrm{2}=\mathrm{0} \\ $$

Question Number 96171 Answers: 0 Comments: 2

(4+(√(15)))^(3/2) −(4−(√(15)))^(3/2) = k(√6) find k

$$\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{4}−\sqrt{\mathrm{15}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\:\mathrm{k}\sqrt{\mathrm{6}} \\ $$$$\mathrm{find}\:\mathrm{k}\: \\ $$

Question Number 96131 Answers: 1 Comments: 0

(((x+4)^2 ))^(1/(3 )) + 4 (((x−3)^2 ))^(1/(3 )) + 5 ((x^2 +x−12))^(1/(3 )) = 0

$$\sqrt[{\mathrm{3}\:\:}]{\left({x}+\mathrm{4}\right)^{\mathrm{2}} }\:+\:\mathrm{4}\:\sqrt[{\mathrm{3}\:\:}]{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:+\:\mathrm{5}\:\sqrt[{\mathrm{3}\:\:}]{{x}^{\mathrm{2}} +{x}−\mathrm{12}}\:=\:\mathrm{0} \\ $$

Pg 262 Pg 263 Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271

Contact: [email protected]