
AlgebraQuestion and Answers: Page 264
Question Number 99698 Answers: 0 Comments: 2

Question Number 99655 Answers: 1 Comments: 1

Question Number 99645 Answers: 1 Comments: 1
Question Number 99621 Answers: 2 Comments: 1
Question Number 99575 Answers: 2 Comments: 0
Question Number 99486 Answers: 0 Comments: 0
Question Number 99430 Answers: 1 Comments: 0

Question Number 99319 Answers: 1 Comments: 0
Question Number 99257 Answers: 2 Comments: 0

Question Number 99256 Answers: 1 Comments: 0
Question Number 99218 Answers: 0 Comments: 3
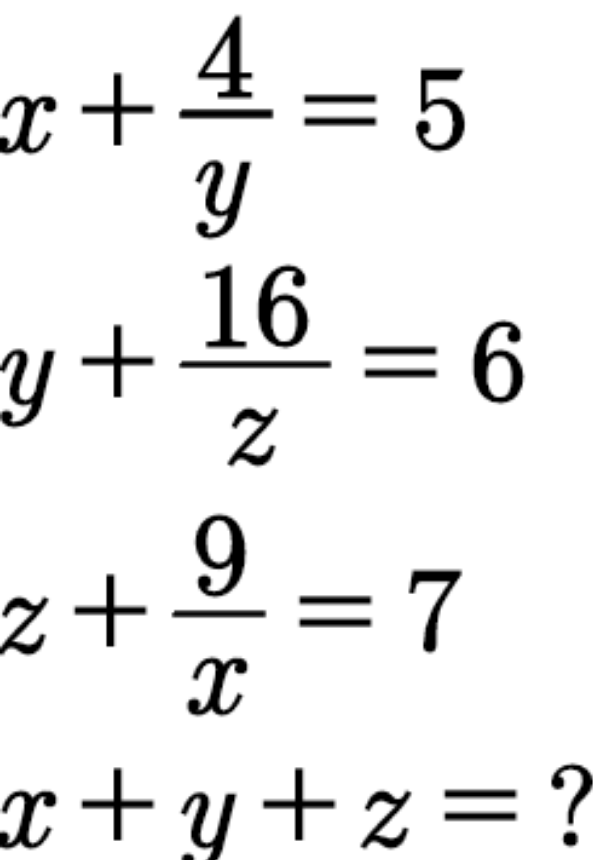
Question Number 99175 Answers: 2 Comments: 0
Question Number 99171 Answers: 0 Comments: 3
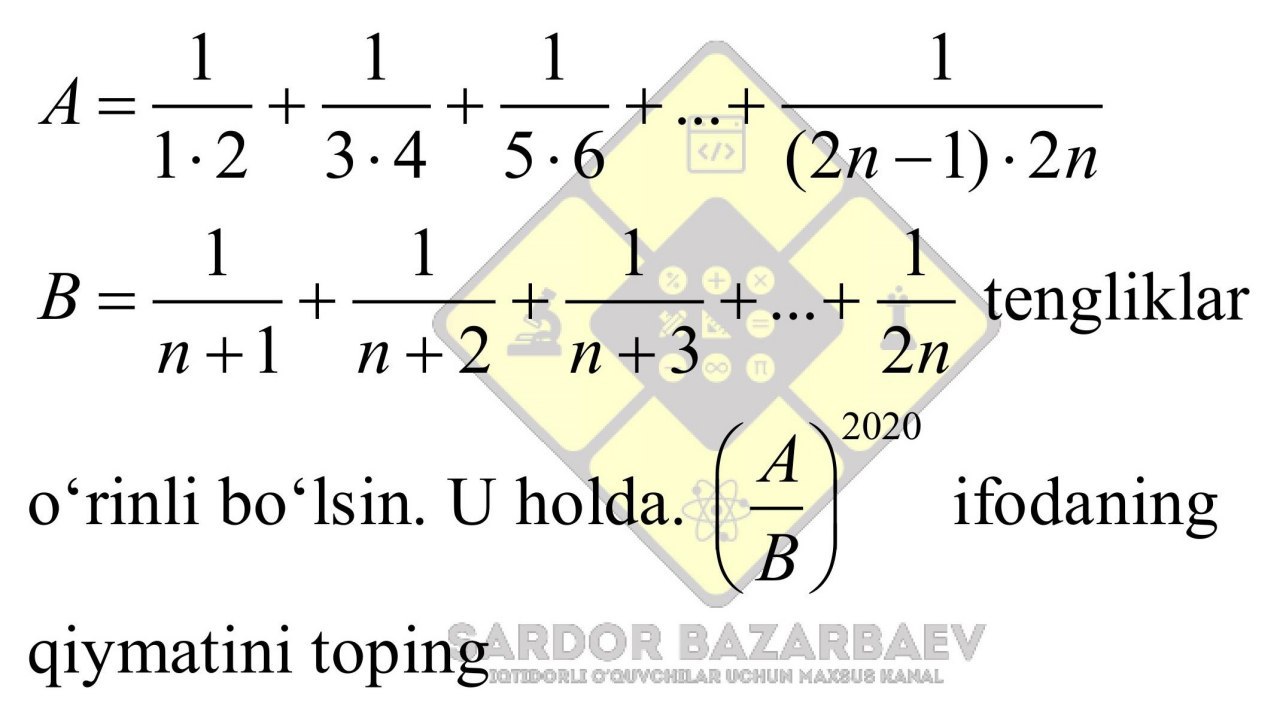
Question Number 99117 Answers: 1 Comments: 0
Question Number 99094 Answers: 1 Comments: 0
Question Number 99089 Answers: 1 Comments: 0
Question Number 99045 Answers: 1 Comments: 0
Question Number 99005 Answers: 2 Comments: 0
Question Number 98983 Answers: 0 Comments: 2
Question Number 98925 Answers: 1 Comments: 1
Question Number 98914 Answers: 3 Comments: 2
Question Number 98859 Answers: 2 Comments: 1

Question Number 98857 Answers: 0 Comments: 0

Question Number 98844 Answers: 3 Comments: 0
Question Number 98842 Answers: 2 Comments: 1
Question Number 98818 Answers: 0 Comments: 0
Pg 259 Pg 260 Pg 261 Pg 262 Pg 263 Pg 264 Pg 265 Pg 266 Pg 267 Pg 268
