
AlgebraQuestion and Answers: Page 263
Question Number 100622 Answers: 0 Comments: 2
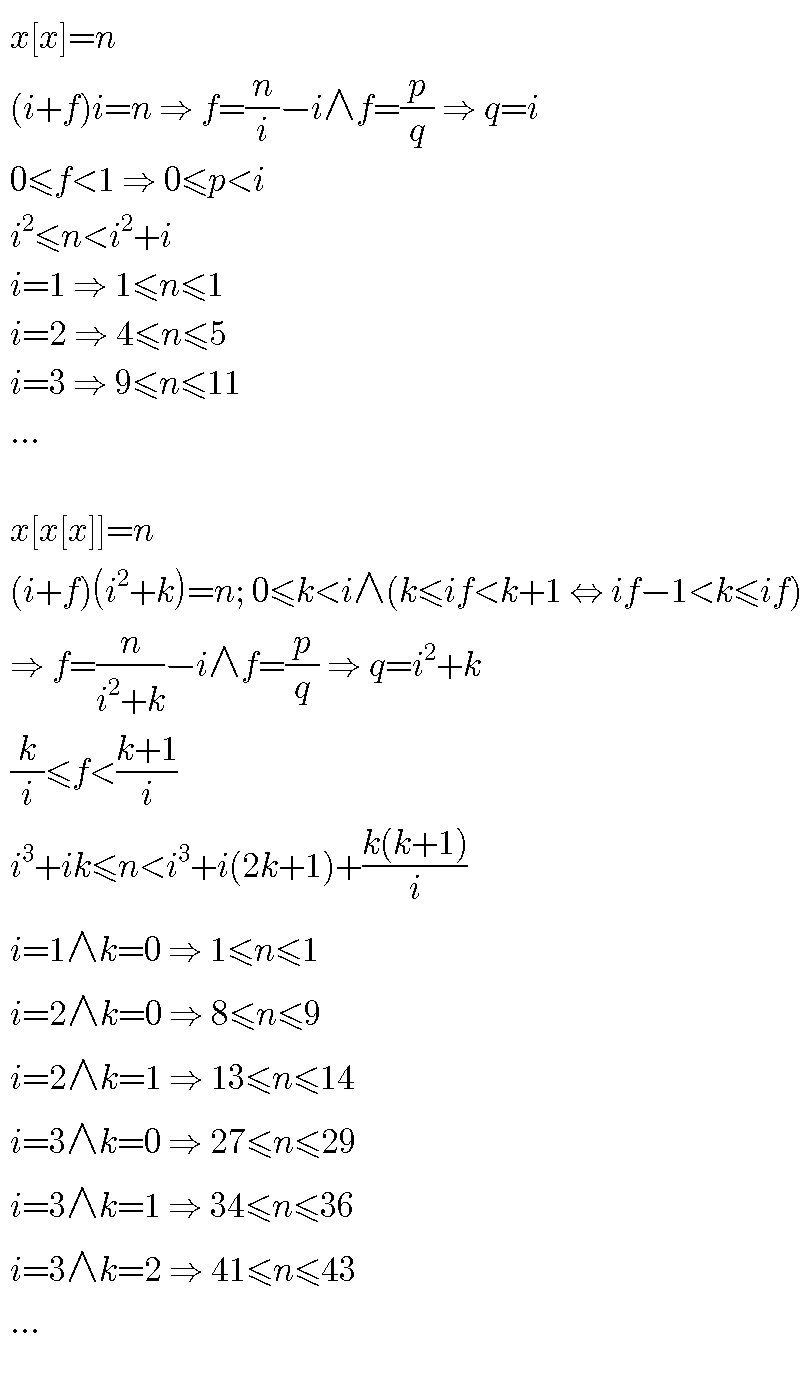
Question Number 100597 Answers: 2 Comments: 1

Question Number 100587 Answers: 2 Comments: 1
Question Number 100567 Answers: 0 Comments: 3
Question Number 100562 Answers: 0 Comments: 0

Question Number 100540 Answers: 0 Comments: 1

Question Number 100492 Answers: 2 Comments: 3
Question Number 100404 Answers: 0 Comments: 11

Question Number 100385 Answers: 1 Comments: 2
Question Number 100330 Answers: 0 Comments: 1
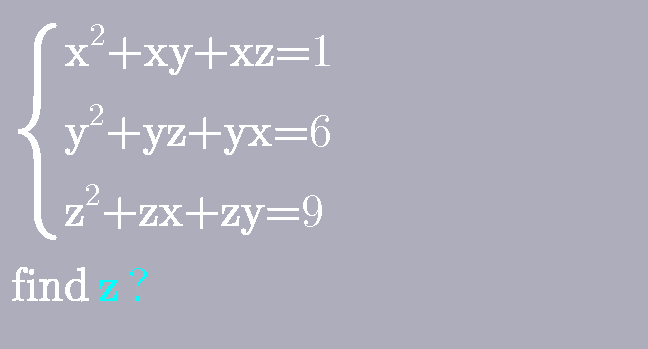
Question Number 100370 Answers: 1 Comments: 2
Question Number 100302 Answers: 0 Comments: 2
Question Number 100198 Answers: 0 Comments: 1

Question Number 100193 Answers: 1 Comments: 3
Question Number 100341 Answers: 1 Comments: 1
Question Number 100040 Answers: 0 Comments: 2

Question Number 100002 Answers: 0 Comments: 0

Question Number 99916 Answers: 1 Comments: 0
Question Number 99900 Answers: 0 Comments: 0
Question Number 99877 Answers: 0 Comments: 5

Question Number 99869 Answers: 2 Comments: 0
Question Number 99846 Answers: 0 Comments: 1
Question Number 99827 Answers: 0 Comments: 0
Question Number 99807 Answers: 3 Comments: 0

Question Number 99803 Answers: 2 Comments: 0
Question Number 99796 Answers: 1 Comments: 0

Pg 258 Pg 259 Pg 260 Pg 261 Pg 262 Pg 263 Pg 264 Pg 265 Pg 266 Pg 267
