
AlgebraQuestion and Answers: Page 259
Question Number 103804 Answers: 0 Comments: 0
Question Number 103736 Answers: 0 Comments: 0
Question Number 103685 Answers: 1 Comments: 0

Question Number 103647 Answers: 0 Comments: 0

Question Number 103603 Answers: 0 Comments: 1

Question Number 103436 Answers: 2 Comments: 0
Question Number 103346 Answers: 0 Comments: 1

Question Number 103345 Answers: 4 Comments: 5

Question Number 103310 Answers: 1 Comments: 1

Question Number 103286 Answers: 3 Comments: 1
Question Number 103278 Answers: 0 Comments: 2
Question Number 103260 Answers: 1 Comments: 0

Question Number 103254 Answers: 0 Comments: 2
Question Number 103253 Answers: 3 Comments: 0
Question Number 103170 Answers: 0 Comments: 3
$${x}^{{x}^{{x}} } =\mathrm{3}\:\:\:\:\:\:{x}=? \\ $$$$ \\ $$
Question Number 103151 Answers: 0 Comments: 1
Question Number 103120 Answers: 0 Comments: 0
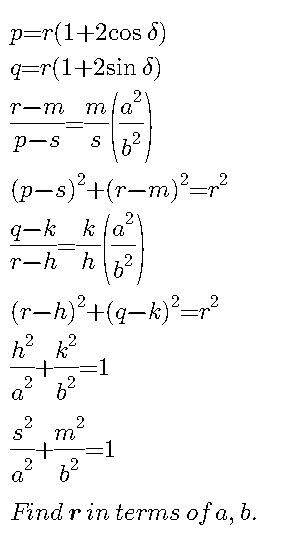
Question Number 103094 Answers: 0 Comments: 4
Question Number 103093 Answers: 5 Comments: 0
Question Number 102975 Answers: 0 Comments: 1
Question Number 102967 Answers: 1 Comments: 0
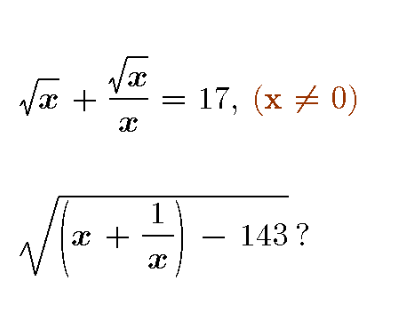
Question Number 102940 Answers: 0 Comments: 1

Question Number 102927 Answers: 3 Comments: 1
Question Number 102548 Answers: 0 Comments: 0
Question Number 102490 Answers: 1 Comments: 0
Question Number 102418 Answers: 1 Comments: 0

Pg 254 Pg 255 Pg 256 Pg 257 Pg 258 Pg 259 Pg 260 Pg 261 Pg 262 Pg 263
