
AlgebraQuestion and Answers: Page 255
Question Number 108295 Answers: 3 Comments: 0
Question Number 108291 Answers: 2 Comments: 0
Question Number 108316 Answers: 3 Comments: 0
Question Number 108270 Answers: 0 Comments: 1
Question Number 108238 Answers: 4 Comments: 0
$${y}={e}^{{x}} {ln}\left({sin}\mathrm{2}{x}\right)\:\:\:\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}=?? \\ $$
Question Number 108237 Answers: 3 Comments: 0
Question Number 108219 Answers: 0 Comments: 3

Question Number 107999 Answers: 3 Comments: 5

Question Number 107976 Answers: 1 Comments: 0
Question Number 107947 Answers: 1 Comments: 0

Question Number 107945 Answers: 3 Comments: 0
Question Number 107867 Answers: 0 Comments: 0

Question Number 107794 Answers: 2 Comments: 0

Question Number 107779 Answers: 1 Comments: 3
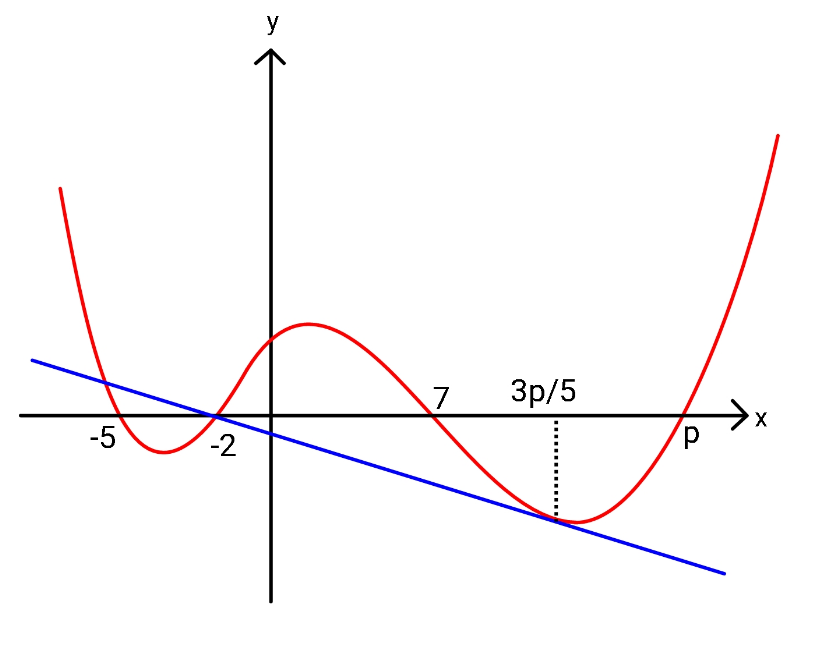
Question Number 107690 Answers: 1 Comments: 0
Question Number 107674 Answers: 2 Comments: 0
$${f}\left({x}\right)=\sqrt{{x}}\sqrt{{x}}\:\:\:\:\:\:\:{D}_{{f}} =??? \\ $$
Question Number 107673 Answers: 3 Comments: 0

Question Number 107486 Answers: 3 Comments: 1
Question Number 107484 Answers: 2 Comments: 0
Question Number 107483 Answers: 2 Comments: 0
Question Number 107454 Answers: 2 Comments: 0
Question Number 107438 Answers: 1 Comments: 0

Question Number 107761 Answers: 0 Comments: 2

Question Number 107385 Answers: 0 Comments: 7
Question Number 107352 Answers: 5 Comments: 0
Question Number 107313 Answers: 2 Comments: 0
Pg 250 Pg 251 Pg 252 Pg 253 Pg 254 Pg 255 Pg 256 Pg 257 Pg 258 Pg 259
