
AlgebraQuestion and Answers: Page 252
Question Number 110399 Answers: 0 Comments: 5
Question Number 110374 Answers: 2 Comments: 0
Question Number 110359 Answers: 1 Comments: 0
Question Number 110318 Answers: 1 Comments: 0
Question Number 110299 Answers: 3 Comments: 0

Question Number 110294 Answers: 1 Comments: 0
Question Number 110269 Answers: 1 Comments: 4

Question Number 110268 Answers: 0 Comments: 3

Question Number 110265 Answers: 0 Comments: 0

Question Number 110246 Answers: 1 Comments: 0
$${solve}\:{for}\:{z}\in\mathbb{C}:\:\left({a}+{bi}\right)^{{z}} ={b}+{ai} \\ $$
Question Number 110219 Answers: 0 Comments: 3
Question Number 110182 Answers: 1 Comments: 2
$$\mathrm{Solve}\:{x}^{\mathrm{3}} +\mathrm{15}{x}−\mathrm{92}=\mathrm{0} \\ $$
Question Number 110173 Answers: 2 Comments: 0
Question Number 110157 Answers: 2 Comments: 0
Question Number 110156 Answers: 1 Comments: 0
Question Number 110136 Answers: 4 Comments: 0
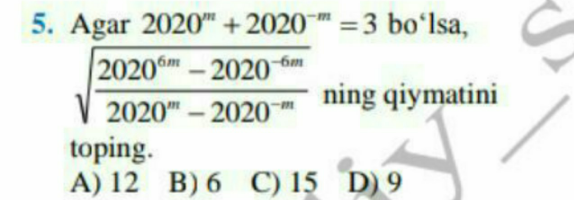
Question Number 110087 Answers: 0 Comments: 3
Question Number 109954 Answers: 1 Comments: 0
Question Number 109914 Answers: 1 Comments: 0
Question Number 109901 Answers: 1 Comments: 0
Question Number 109895 Answers: 1 Comments: 3
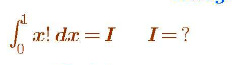
Question Number 109754 Answers: 1 Comments: 0
Question Number 109721 Answers: 1 Comments: 0
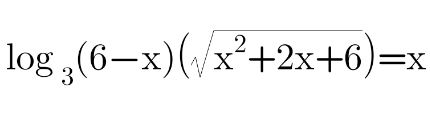
Question Number 109699 Answers: 1 Comments: 0
Question Number 109626 Answers: 1 Comments: 1

Question Number 109625 Answers: 0 Comments: 2
Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 Pg 254 Pg 255 Pg 256
