
AlgebraQuestion and Answers: Page 250
Question Number 112097 Answers: 0 Comments: 2
$$\:\:\:\:\:\:\mid\mid{x}−\mathrm{1}\mid+\mathrm{1}\mid\:<\:{x} \\ $$
Question Number 112087 Answers: 2 Comments: 0
Question Number 112065 Answers: 1 Comments: 0
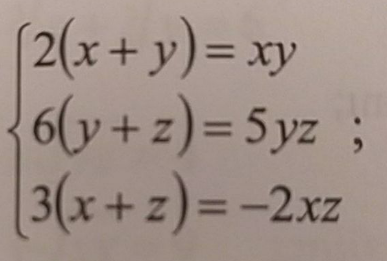
Question Number 112058 Answers: 1 Comments: 0

Question Number 112053 Answers: 1 Comments: 1
Question Number 112008 Answers: 0 Comments: 0

Question Number 111939 Answers: 2 Comments: 0

Question Number 111982 Answers: 2 Comments: 0

Question Number 111909 Answers: 2 Comments: 0
Question Number 111724 Answers: 0 Comments: 6
Question Number 111623 Answers: 1 Comments: 2
Question Number 111601 Answers: 1 Comments: 0
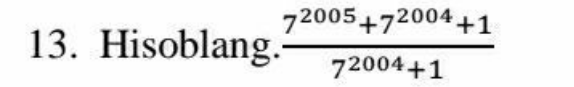
Question Number 111586 Answers: 0 Comments: 3
Question Number 111583 Answers: 1 Comments: 0
Question Number 111560 Answers: 2 Comments: 1

Question Number 111534 Answers: 2 Comments: 0
Question Number 111365 Answers: 0 Comments: 0

Question Number 111344 Answers: 0 Comments: 3
Question Number 111343 Answers: 0 Comments: 1
Question Number 111208 Answers: 1 Comments: 3
Question Number 111175 Answers: 1 Comments: 0
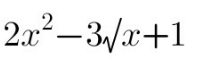
Question Number 111134 Answers: 0 Comments: 0
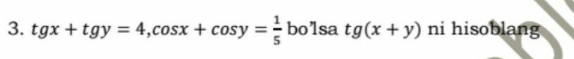
Question Number 111062 Answers: 0 Comments: 2

Question Number 111029 Answers: 1 Comments: 0
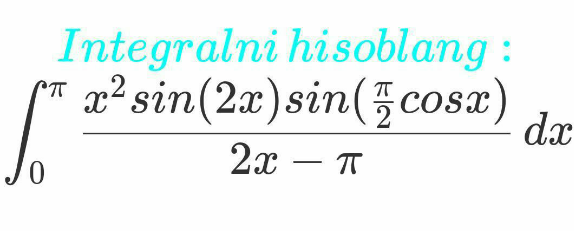
Question Number 111008 Answers: 0 Comments: 3
Question Number 110897 Answers: 3 Comments: 0
Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 Pg 254
