
AlgebraQuestion and Answers: Page 249
Question Number 112803 Answers: 1 Comments: 0
Question Number 112802 Answers: 3 Comments: 0
Question Number 112796 Answers: 0 Comments: 2
Question Number 112795 Answers: 1 Comments: 1

Question Number 112626 Answers: 1 Comments: 0
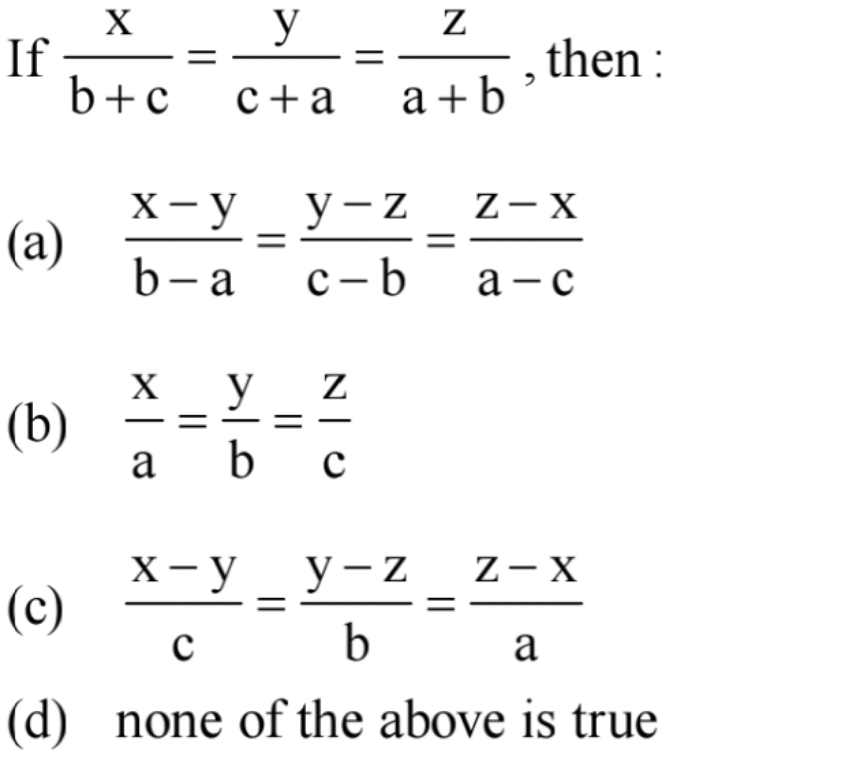
Question Number 112625 Answers: 4 Comments: 1
Question Number 112624 Answers: 3 Comments: 0
Question Number 112528 Answers: 0 Comments: 2
Question Number 112509 Answers: 0 Comments: 1

Question Number 112478 Answers: 1 Comments: 0
Question Number 112464 Answers: 1 Comments: 0

Question Number 112461 Answers: 1 Comments: 0
Question Number 112408 Answers: 0 Comments: 1
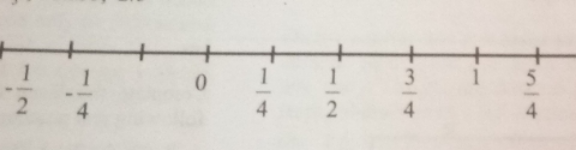
Question Number 112360 Answers: 1 Comments: 1
Question Number 112280 Answers: 2 Comments: 0
Question Number 112097 Answers: 0 Comments: 2
$$\:\:\:\:\:\:\mid\mid{x}−\mathrm{1}\mid+\mathrm{1}\mid\:<\:{x} \\ $$
Question Number 112087 Answers: 2 Comments: 0
Question Number 112065 Answers: 1 Comments: 0
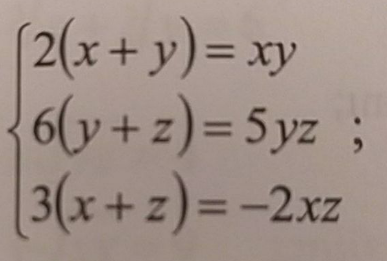
Question Number 112058 Answers: 1 Comments: 0

Question Number 112053 Answers: 1 Comments: 1
Question Number 112008 Answers: 0 Comments: 0

Question Number 111939 Answers: 2 Comments: 0

Question Number 111982 Answers: 2 Comments: 0

Question Number 111909 Answers: 2 Comments: 0
Question Number 111724 Answers: 0 Comments: 6
Question Number 111623 Answers: 1 Comments: 2
Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253
