
AlgebraQuestion and Answers: Page 247
Question Number 115135 Answers: 1 Comments: 1
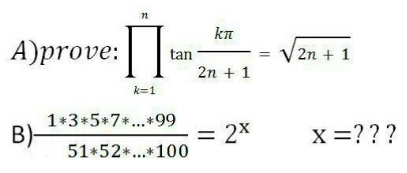
Question Number 115023 Answers: 2 Comments: 0
Question Number 115018 Answers: 2 Comments: 0
Question Number 114956 Answers: 0 Comments: 5

Question Number 114919 Answers: 0 Comments: 0

Question Number 114912 Answers: 0 Comments: 0

Question Number 114917 Answers: 0 Comments: 3

Question Number 114809 Answers: 1 Comments: 1
Question Number 114806 Answers: 1 Comments: 0

Question Number 114799 Answers: 1 Comments: 0

Question Number 114796 Answers: 2 Comments: 0

Question Number 114795 Answers: 1 Comments: 0

Question Number 114758 Answers: 1 Comments: 0
Question Number 114739 Answers: 1 Comments: 0
Question Number 114720 Answers: 2 Comments: 0
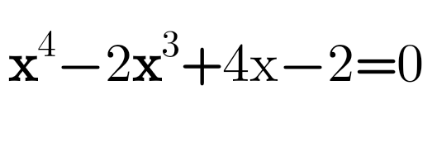
Question Number 114653 Answers: 2 Comments: 0
Question Number 114625 Answers: 1 Comments: 0
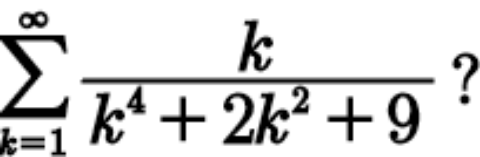
Question Number 114593 Answers: 1 Comments: 0
$$\frac{\mid{x}−\mathrm{1}\mid}{\mid{x}\mid−\mathrm{1}}\:\leqslant\:\mathrm{1} \\ $$
Question Number 114592 Answers: 3 Comments: 0
Question Number 114551 Answers: 1 Comments: 3
Question Number 114538 Answers: 1 Comments: 4
Question Number 114511 Answers: 2 Comments: 3
Question Number 114388 Answers: 0 Comments: 2
Question Number 114189 Answers: 0 Comments: 6

Question Number 114134 Answers: 1 Comments: 4
Question Number 114110 Answers: 1 Comments: 2
Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251
