
AlgebraQuestion and Answers: Page 239
Question Number 120839 Answers: 3 Comments: 0
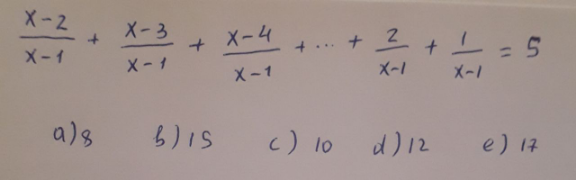
Question Number 120809 Answers: 0 Comments: 0
Question Number 120780 Answers: 2 Comments: 2
$${solve}\:{x}^{\mathrm{2}^{{x}} } =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Question Number 120711 Answers: 3 Comments: 0
Question Number 120636 Answers: 0 Comments: 23
Question Number 120601 Answers: 1 Comments: 0
Question Number 120583 Answers: 0 Comments: 0
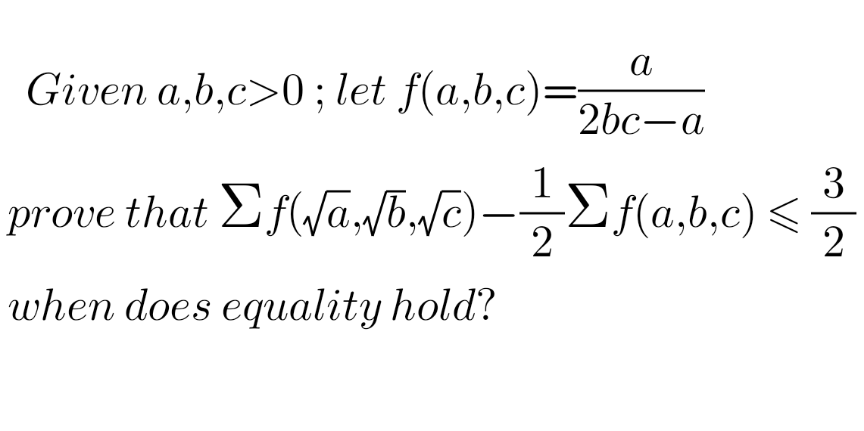
Question Number 120558 Answers: 3 Comments: 0
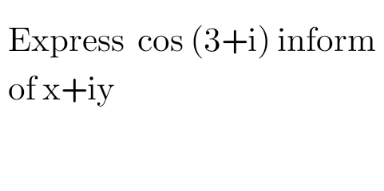
Question Number 120556 Answers: 0 Comments: 2

Question Number 120545 Answers: 1 Comments: 2
Question Number 120529 Answers: 1 Comments: 1

Question Number 120480 Answers: 4 Comments: 0
Question Number 120475 Answers: 1 Comments: 0

Question Number 120472 Answers: 0 Comments: 0
Question Number 120471 Answers: 1 Comments: 0
Question Number 120470 Answers: 0 Comments: 0
Question Number 120469 Answers: 1 Comments: 0
Question Number 120464 Answers: 1 Comments: 0
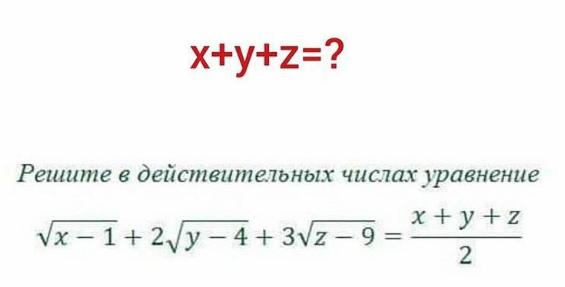
Question Number 120455 Answers: 0 Comments: 0

Question Number 120355 Answers: 3 Comments: 2

Question Number 120325 Answers: 0 Comments: 6
Question Number 120324 Answers: 1 Comments: 0
Question Number 120240 Answers: 1 Comments: 0
Question Number 120229 Answers: 2 Comments: 0

Question Number 120228 Answers: 0 Comments: 0
Question Number 120185 Answers: 1 Comments: 0
$${solve}\:{for}\:{x},\:{y}\in{Z} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{\mathrm{2020}} \\ $$
Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243
