
AlgebraQuestion and Answers: Page 238
Question Number 122551 Answers: 1 Comments: 0

Question Number 122523 Answers: 2 Comments: 0
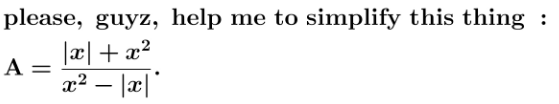
Question Number 122445 Answers: 2 Comments: 0

Question Number 122360 Answers: 3 Comments: 0
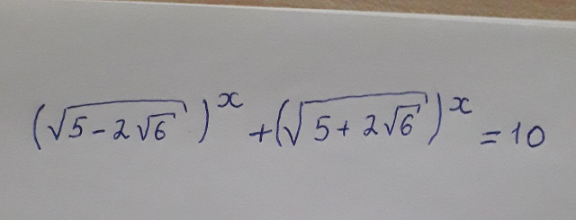
Question Number 122214 Answers: 1 Comments: 0
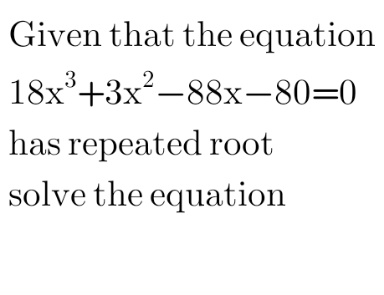
Question Number 122166 Answers: 3 Comments: 0
Question Number 122095 Answers: 0 Comments: 0
Question Number 122081 Answers: 2 Comments: 0
Question Number 122075 Answers: 1 Comments: 0

Question Number 122012 Answers: 0 Comments: 1
$${r}\mathrm{4}{width}\mathrm{10}{calculatesurfacearea} \\ $$
Question Number 122010 Answers: 1 Comments: 0

Question Number 122002 Answers: 2 Comments: 0
Question Number 121996 Answers: 1 Comments: 0
Question Number 122174 Answers: 1 Comments: 0
Question Number 121973 Answers: 1 Comments: 4
Question Number 121957 Answers: 0 Comments: 4
Question Number 121950 Answers: 1 Comments: 0
Question Number 121948 Answers: 0 Comments: 0

Question Number 121919 Answers: 2 Comments: 0
Question Number 121918 Answers: 1 Comments: 6
Question Number 121913 Answers: 1 Comments: 0
Question Number 121890 Answers: 2 Comments: 1

Question Number 121889 Answers: 2 Comments: 0

Question Number 121847 Answers: 0 Comments: 0

Question Number 121754 Answers: 2 Comments: 0
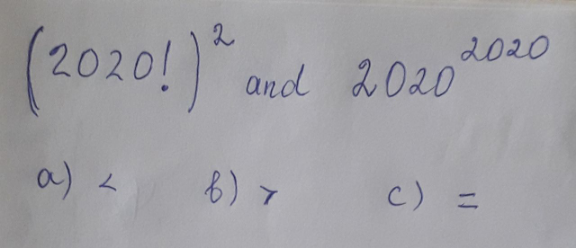
Question Number 121720 Answers: 2 Comments: 0
Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242
