
AlgebraQuestion and Answers: Page 237
Question Number 123175 Answers: 1 Comments: 0
Question Number 123114 Answers: 2 Comments: 2
Question Number 123108 Answers: 0 Comments: 2

Question Number 123053 Answers: 0 Comments: 0
Question Number 123039 Answers: 1 Comments: 0
Question Number 123062 Answers: 1 Comments: 0
Question Number 123025 Answers: 1 Comments: 4
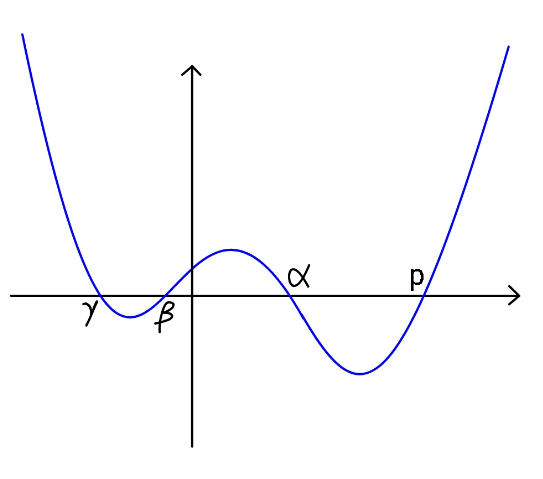
Question Number 123024 Answers: 1 Comments: 0

Question Number 122957 Answers: 1 Comments: 1
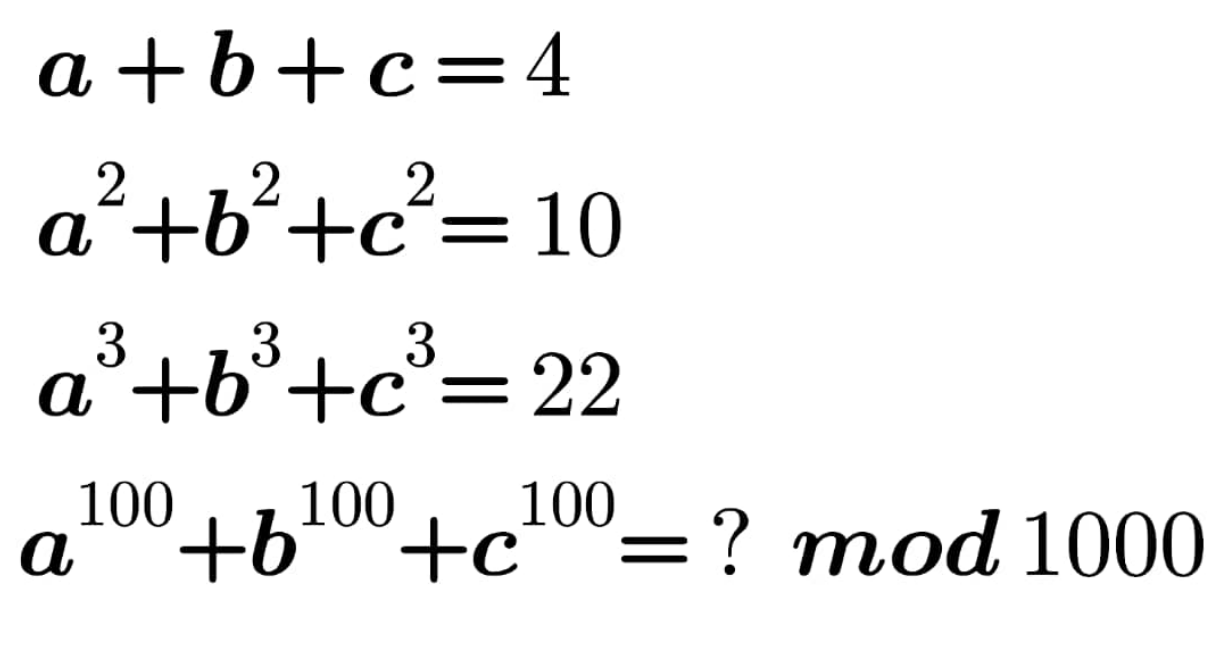
Question Number 122950 Answers: 0 Comments: 1
Question Number 122897 Answers: 2 Comments: 0
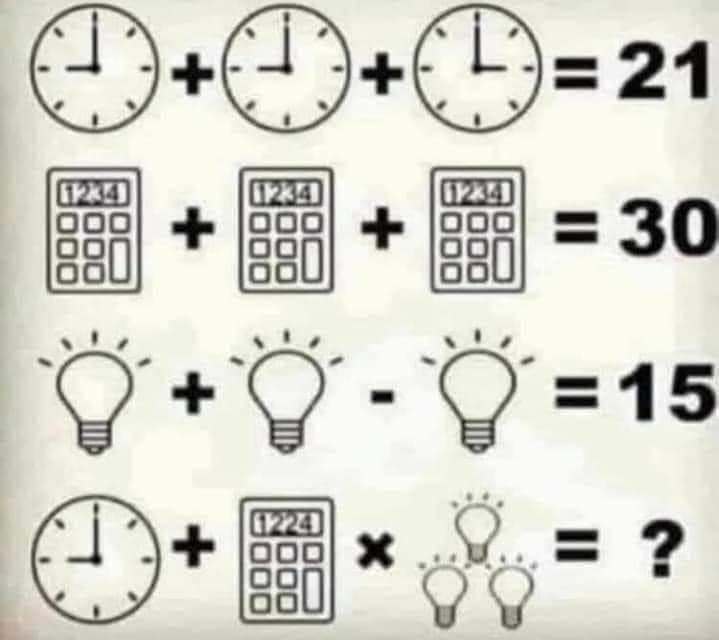
Question Number 122883 Answers: 4 Comments: 2
Question Number 122860 Answers: 1 Comments: 0

Question Number 122861 Answers: 0 Comments: 3
Question Number 122857 Answers: 0 Comments: 0

Question Number 122854 Answers: 1 Comments: 0

Question Number 122821 Answers: 1 Comments: 0
Question Number 122658 Answers: 0 Comments: 0
Question Number 122653 Answers: 1 Comments: 0
Question Number 122651 Answers: 1 Comments: 0
Question Number 122649 Answers: 1 Comments: 2
Question Number 122648 Answers: 2 Comments: 0
Question Number 122647 Answers: 0 Comments: 0
Question Number 122646 Answers: 0 Comments: 4
Question Number 122640 Answers: 0 Comments: 0
Question Number 122580 Answers: 0 Comments: 3
Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241
