
AlgebraQuestion and Answers: Page 236
Question Number 124109 Answers: 1 Comments: 0
Question Number 124108 Answers: 1 Comments: 0
Question Number 124107 Answers: 0 Comments: 0
Question Number 124106 Answers: 0 Comments: 0
Question Number 124056 Answers: 0 Comments: 2
Question Number 123987 Answers: 1 Comments: 0
Question Number 123894 Answers: 2 Comments: 0

Question Number 123886 Answers: 1 Comments: 0
Question Number 123824 Answers: 1 Comments: 1
Question Number 123746 Answers: 0 Comments: 1
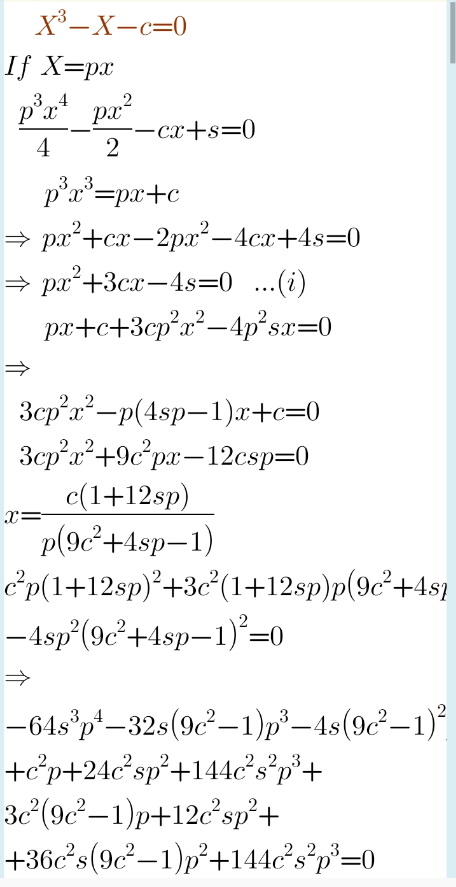
Question Number 123638 Answers: 0 Comments: 1
Question Number 123626 Answers: 0 Comments: 0
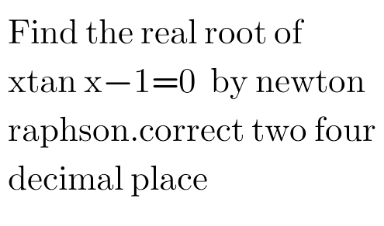
Question Number 123595 Answers: 0 Comments: 1
Question Number 123591 Answers: 0 Comments: 2
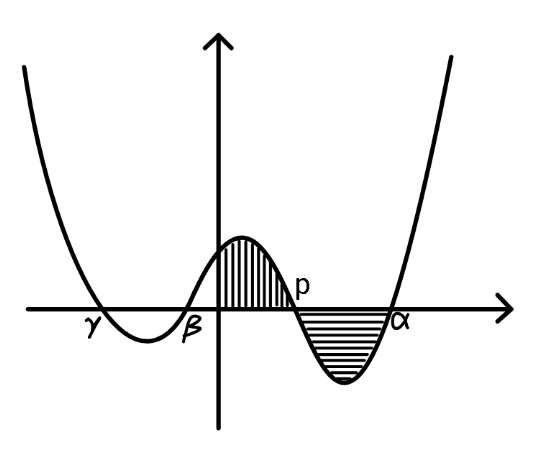
Question Number 123576 Answers: 1 Comments: 2

Question Number 123574 Answers: 1 Comments: 0

Question Number 123548 Answers: 1 Comments: 1
Question Number 123510 Answers: 0 Comments: 0
Question Number 123509 Answers: 1 Comments: 0
$$\underset{−\frac{\pi}{}\mathrm{2}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mid{cosx}\mid=? \\ $$
Question Number 123426 Answers: 0 Comments: 5
Question Number 123409 Answers: 1 Comments: 0
Question Number 123362 Answers: 1 Comments: 0

Question Number 123265 Answers: 2 Comments: 2

Question Number 123175 Answers: 1 Comments: 0
Question Number 123114 Answers: 2 Comments: 2
Question Number 123108 Answers: 0 Comments: 2

Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240
