
AlgebraQuestion and Answers: Page 235
Question Number 125131 Answers: 0 Comments: 0
Question Number 125107 Answers: 0 Comments: 1

Question Number 124988 Answers: 1 Comments: 3

Question Number 124963 Answers: 2 Comments: 1
Question Number 124907 Answers: 0 Comments: 0

Question Number 125185 Answers: 1 Comments: 0
Question Number 124820 Answers: 1 Comments: 0

Question Number 124797 Answers: 2 Comments: 0

Question Number 124791 Answers: 1 Comments: 1

Question Number 124740 Answers: 1 Comments: 1
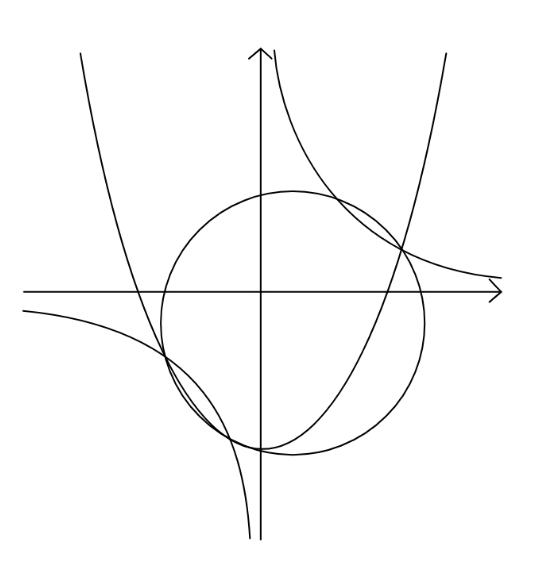
Question Number 124617 Answers: 0 Comments: 0

Question Number 124567 Answers: 1 Comments: 0
Question Number 124522 Answers: 1 Comments: 0
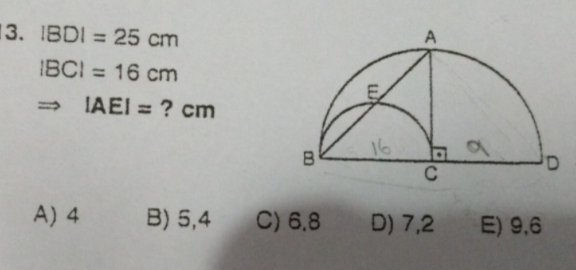
Question Number 124496 Answers: 0 Comments: 0
Question Number 124458 Answers: 0 Comments: 0

Question Number 124387 Answers: 1 Comments: 0
Question Number 124375 Answers: 0 Comments: 0

Question Number 124314 Answers: 0 Comments: 1
Question Number 124312 Answers: 1 Comments: 0
Question Number 124240 Answers: 0 Comments: 0
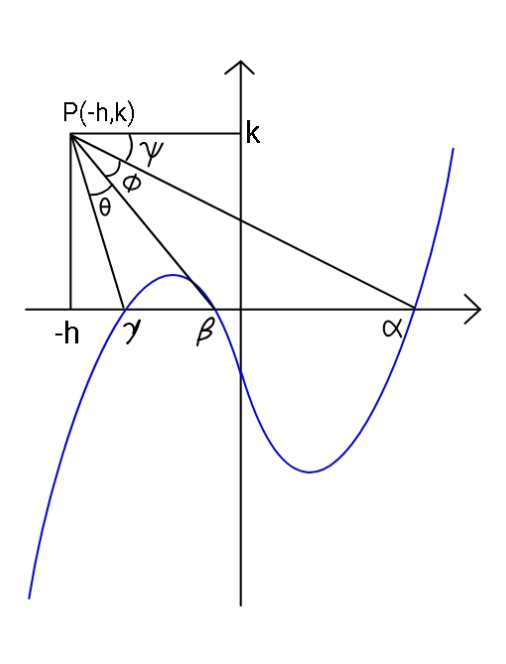
Question Number 124210 Answers: 2 Comments: 0
Question Number 124149 Answers: 1 Comments: 4
Question Number 124110 Answers: 2 Comments: 0
Question Number 124109 Answers: 1 Comments: 0
Question Number 124108 Answers: 1 Comments: 0
Question Number 124107 Answers: 0 Comments: 0
Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239
