Question and Answers Forum

AlgebraQuestion and Answers: Page 234

Question Number 121552 Answers: 0 Comments: 5

Question Number 121538 Answers: 1 Comments: 0

Question Number 121449 Answers: 3 Comments: 1

{ ((x+y=3)),((x^5 +y^5 =33)) :}

$$\:\:\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{3}}\\{\mathrm{x}^{\mathrm{5}} +\mathrm{y}^{\mathrm{5}} =\mathrm{33}}\end{cases} \\ $$

Question Number 121446 Answers: 3 Comments: 0

Question Number 121444 Answers: 0 Comments: 3

6^x^2 +81.4^x ≤ 4^x .3^x^2 + 81.2^x^2

$$\:\mathrm{6}^{\mathrm{x}^{\mathrm{2}} } +\mathrm{81}.\mathrm{4}^{\mathrm{x}} \:\leqslant\:\mathrm{4}^{\mathrm{x}} .\mathrm{3}^{\mathrm{x}^{\mathrm{2}} } +\:\mathrm{81}.\mathrm{2}^{\mathrm{x}^{\mathrm{2}} } \\ $$

Question Number 121442 Answers: 2 Comments: 0

Question Number 121429 Answers: 0 Comments: 1

Question Number 121423 Answers: 2 Comments: 0

x^4 −2(√2)x^2 −x+2−(√2)=0 x=?

$${x}^{\mathrm{4}} −\mathrm{2}\sqrt{\mathrm{2}}{x}^{\mathrm{2}} −{x}+\mathrm{2}−\sqrt{\mathrm{2}}=\mathrm{0}\:\:\:{x}=? \\ $$

Question Number 121359 Answers: 0 Comments: 0

Find all n∈N such that (n+3)^n = Σ_(k=3) ^(n+2) k^n

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{n}\in\mathbb{N}\:\mathrm{such}\:\mathrm{that}\:\left(\mathrm{n}+\mathrm{3}\right)^{\mathrm{n}} \:=\:\underset{\mathrm{k}=\mathrm{3}} {\overset{\mathrm{n}+\mathrm{2}} {\sum}}\:\mathrm{k}^{\mathrm{n}} \\ $$

Question Number 121257 Answers: 2 Comments: 4

If today is June 17,2009 and George was born on November 25, 1967. How old is George?

$$\mathrm{If}\:\mathrm{today}\:\mathrm{is}\:\mathrm{June}\:\mathrm{17},\mathrm{2009}\:\mathrm{and}\:\mathrm{George} \\ $$$$\mathrm{was}\:\mathrm{born}\:\mathrm{on}\:\mathrm{November}\:\mathrm{25},\:\mathrm{1967}.\: \\ $$$$\mathrm{How}\:\mathrm{old}\:\mathrm{is}\:\mathrm{George}? \\ $$

Question Number 121246 Answers: 2 Comments: 0

Σ_(k=1) ^(49) (1/( (√(k+(√(k^2 −1)))))) ?

$$\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{k}+\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}}\:? \\ $$

Question Number 121199 Answers: 0 Comments: 0

Question Number 121170 Answers: 0 Comments: 0

(a;b;c)∈∀ a^a ∙ b^b ∙ c^c ≥(abc)^((a+b+c)/3)

$$\:\:\:\:\:\:\left(\boldsymbol{{a}};\boldsymbol{{b}};\boldsymbol{{c}}\right)\in\forall \\ $$$$\:\boldsymbol{{a}}^{\boldsymbol{{a}}} \centerdot\:\boldsymbol{{b}}^{\boldsymbol{{b}}} \centerdot\:\boldsymbol{{c}}^{\boldsymbol{{c}}} \geqslant\left(\boldsymbol{{abc}}\right)^{\frac{\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}}{\mathrm{3}}} \\ $$

Question Number 121136 Answers: 2 Comments: 1

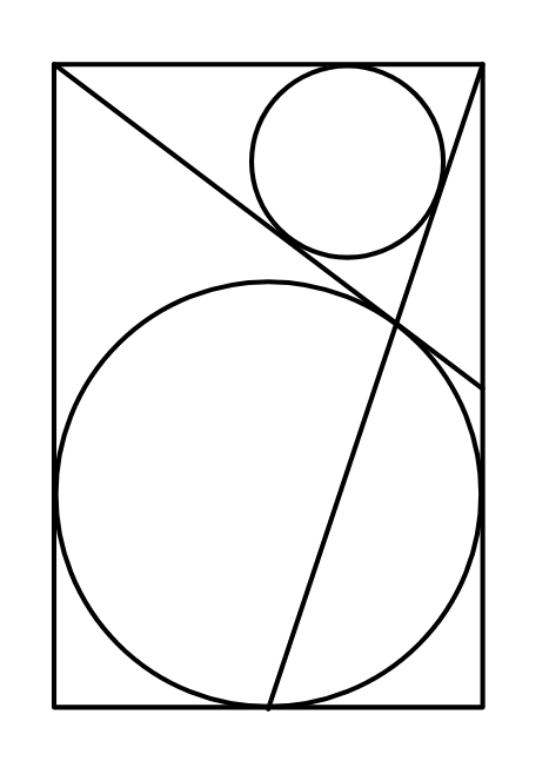
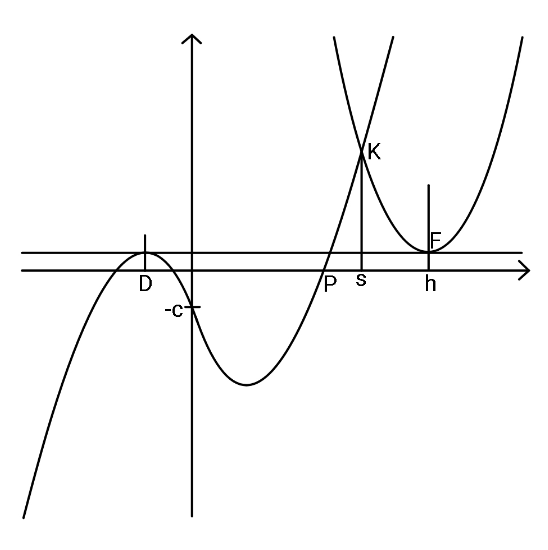
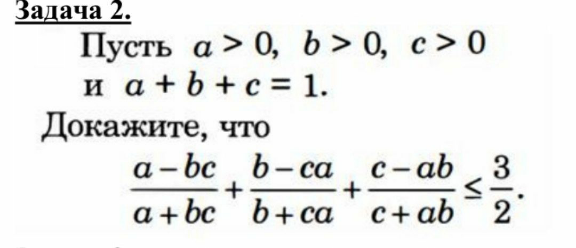
Question Number 121127 Answers: 3 Comments: 0

(√(3+2i))=?

$$\sqrt{\mathrm{3}+\mathrm{2}{i}}=? \\ $$

Question Number 121099 Answers: 1 Comments: 0

Let α be a root of x^5 −x^3 +x−2=0 Then prove that [α^6 ]=3 where[λ] denotes greatest integer less than or equal λ

$${Let}\:\alpha\:{be}\:{a}\:{root}\:{of}\:\:{x}^{\mathrm{5}} −{x}^{\mathrm{3}} +{x}−\mathrm{2}=\mathrm{0} \\ $$$${Then}\:{prove}\:{that}\:\:\:\left[\alpha^{\mathrm{6}} \right]=\mathrm{3}\:\:\:\:\:\:\:{where}\left[\lambda\right]\:\:{denotes}\:{greatest}\:{integer} \\ $$$${less}\:{than}\:{or}\:\:{equal}\:\lambda \\ $$

Question Number 121041 Answers: 1 Comments: 0

Σ_(k=1) ^n (−1)^k .k =?

$$\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} .\mathrm{k}\:=?\: \\ $$

Question Number 120993 Answers: 0 Comments: 0

Question Number 120984 Answers: 2 Comments: 0

(1/(1∙4∙7)) + (1/(4∙7∙10))+(1/(7∙10∙13))+...+(1/(25∙28∙31))= ?

$$\frac{\mathrm{1}}{\mathrm{1}\centerdot\mathrm{4}\centerdot\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{4}\centerdot\mathrm{7}\centerdot\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{7}\centerdot\mathrm{10}\centerdot\mathrm{13}}+...+\frac{\mathrm{1}}{\mathrm{25}\centerdot\mathrm{28}\centerdot\mathrm{31}}=\:? \\ $$

Question Number 120960 Answers: 0 Comments: 0

If x,y,z>0 then prove following inequality (x^2 +2)(y^2 +2)(z^2 +2)≥9(xy+yz+xz)

$${If}\:{x},{y},{z}>\mathrm{0}\:\:{then}\:{prove}\:{following} \\ $$$${inequality} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({y}^{\mathrm{2}} +\mathrm{2}\right)\left({z}^{\mathrm{2}} +\mathrm{2}\right)\geqslant\mathrm{9}\left({xy}+{yz}+{xz}\right) \\ $$

Question Number 120953 Answers: 4 Comments: 0

solve in x∈R ∣ 3x−4 ∣ = x−5

$$\mathrm{solve}\:\mathrm{in}\:\mathrm{x}\in\mathbb{R} \\ $$$$\mid\:\mathrm{3x}−\mathrm{4}\:\mid\:=\:\mathrm{x}−\mathrm{5}\: \\ $$

Question Number 120943 Answers: 3 Comments: 1

∫(x^3 +3)^4 dx=?

$$\int\left({x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{4}} {dx}=? \\ $$

Question Number 120929 Answers: 5 Comments: 2

Question Number 120904 Answers: 1 Comments: 1

Question Number 120882 Answers: 1 Comments: 0

Question Number 120855 Answers: 2 Comments: 0

... elementary calculus... :: α,β are roots of equation of : x^2 −6x−2=0 define :: t_n =α^n −β^n (n≥1) then evaluate : A=((t_(10) −2t_8 )/(2t_9 )) =??? ...m.n.1970...

$$\:\:\:\:\:\:\:\:\:\:\:...\:{elementary}\:\:{calculus}... \\ $$$$\:\:::\:\alpha,\beta\:{are}\:{roots}\:{of}\:\:{equation} \\ $$$$\:\:\:\:\:{of}\::\:{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{define}\:::\:{t}_{{n}} =\alpha^{{n}} −\beta^{{n}} \:\left({n}\geqslant\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{then}\:\:{evaluate}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\frac{{t}_{\mathrm{10}} −\mathrm{2}{t}_{\mathrm{8}} }{\mathrm{2}{t}_{\mathrm{9}} }\:=??? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}.\mathrm{1970}... \\ $$

Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238

Contact: info@tinkutara.com