
AlgebraQuestion and Answers: Page 233
Question Number 126930 Answers: 1 Comments: 4
$$\:\:\sqrt{\mathrm{1997}×\mathrm{1996}×\mathrm{1995}×\mathrm{1994}+\mathrm{1}}\:=? \\ $$
Question Number 126887 Answers: 2 Comments: 2
Question Number 126882 Answers: 1 Comments: 0
Question Number 126845 Answers: 3 Comments: 0
Question Number 126723 Answers: 0 Comments: 2

Question Number 126702 Answers: 1 Comments: 0
Question Number 126701 Answers: 2 Comments: 0
Question Number 126700 Answers: 2 Comments: 0
Question Number 126619 Answers: 2 Comments: 0
Question Number 126504 Answers: 0 Comments: 0

Question Number 126484 Answers: 0 Comments: 6

Question Number 126482 Answers: 1 Comments: 0

Question Number 126430 Answers: 3 Comments: 1
Question Number 126391 Answers: 3 Comments: 0
Question Number 126363 Answers: 2 Comments: 0
Question Number 126329 Answers: 1 Comments: 0

Question Number 126180 Answers: 2 Comments: 0
$${solve}\:\mid\:\mid{x}−\mathrm{1}\mid\:−\mathrm{2}\mid\:=\:\mid\:{x}−\mathrm{3}\:\mid\: \\ $$
Question Number 126165 Answers: 0 Comments: 1
Question Number 126161 Answers: 3 Comments: 0
Question Number 126109 Answers: 2 Comments: 0
Question Number 126105 Answers: 1 Comments: 1
Question Number 126104 Answers: 0 Comments: 1
Question Number 126030 Answers: 1 Comments: 0
$$\mathrm{2}^{\mathrm{x}} =\mathrm{4x} \\ $$$$\mathrm{solve}\:\mathrm{it}\:\mathrm{please} \\ $$
Question Number 125990 Answers: 0 Comments: 0
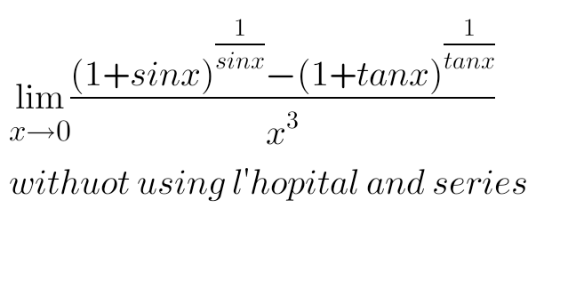
Question Number 125960 Answers: 2 Comments: 0
Question Number 125947 Answers: 0 Comments: 0

Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237
