
AlgebraQuestion and Answers: Page 230
Question Number 129310 Answers: 0 Comments: 1

Question Number 129300 Answers: 2 Comments: 0
Question Number 129279 Answers: 0 Comments: 3
Question Number 129255 Answers: 0 Comments: 1
$$\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} =? \\ $$
Question Number 129235 Answers: 2 Comments: 2
Question Number 129148 Answers: 0 Comments: 1
Question Number 128942 Answers: 2 Comments: 0
Question Number 128932 Answers: 1 Comments: 3
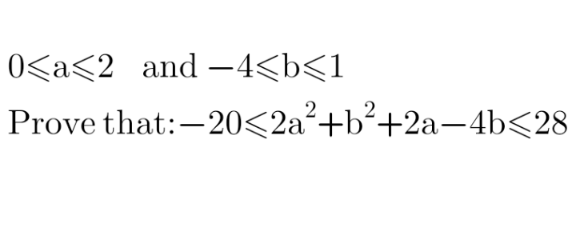
Question Number 128918 Answers: 0 Comments: 2

Question Number 128903 Answers: 2 Comments: 0
Question Number 128850 Answers: 1 Comments: 0
Question Number 128715 Answers: 0 Comments: 1
Question Number 128712 Answers: 2 Comments: 1
Question Number 128698 Answers: 1 Comments: 3
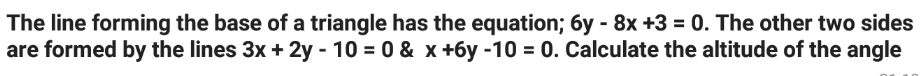
Question Number 128684 Answers: 1 Comments: 0
$${how}\:{we}\:{can}\:{convert}\:\mathrm{0}.\overset{−} {\mathrm{9}}\:{to}\:\frac{{q}}{{p}}? \\ $$
Question Number 128636 Answers: 1 Comments: 0
Question Number 128632 Answers: 0 Comments: 0
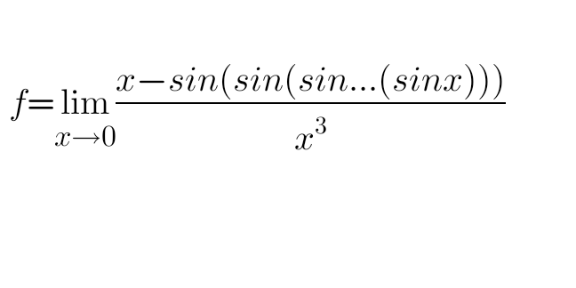
Question Number 128617 Answers: 1 Comments: 1
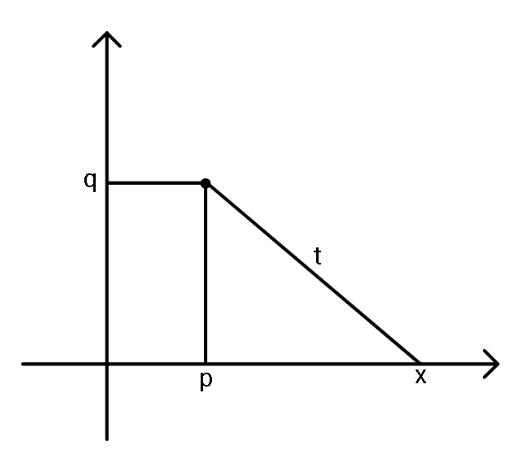
Question Number 128589 Answers: 1 Comments: 0
Question Number 128509 Answers: 1 Comments: 0

Question Number 128508 Answers: 1 Comments: 0
$${if}\:\:{x}^{{x}^{\mathrm{3}} } =\mathrm{3} \\ $$$${find}\:{x} \\ $$
Question Number 128457 Answers: 0 Comments: 1
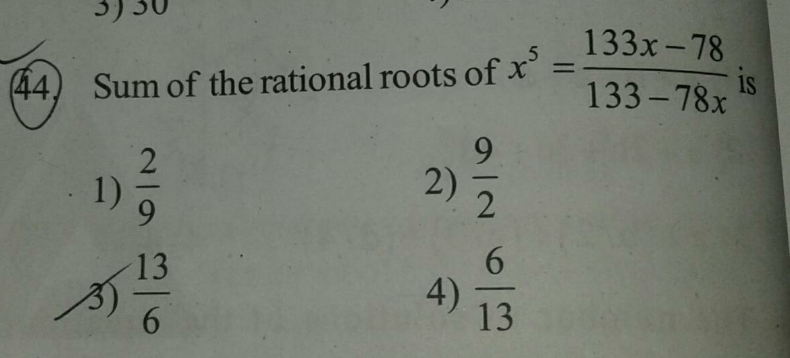
Question Number 128459 Answers: 1 Comments: 0
Question Number 128388 Answers: 0 Comments: 1
Question Number 128458 Answers: 0 Comments: 1

Question Number 128371 Answers: 1 Comments: 1
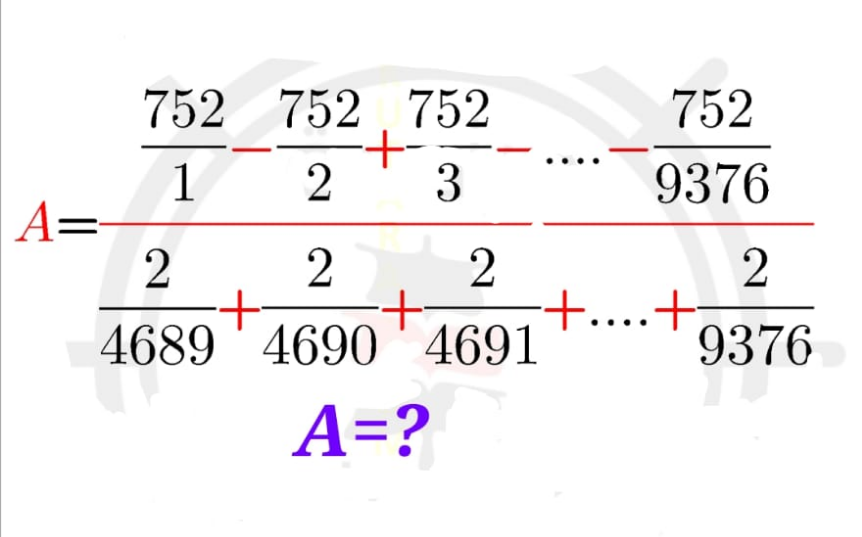
Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234
