
AlgebraQuestion and Answers: Page 229
Question Number 128850 Answers: 1 Comments: 0
Question Number 128715 Answers: 0 Comments: 1
Question Number 128712 Answers: 2 Comments: 1
Question Number 128698 Answers: 1 Comments: 3
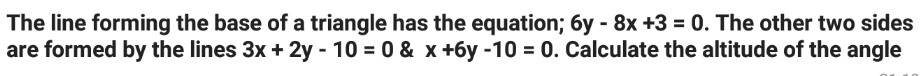
Question Number 128684 Answers: 1 Comments: 0
$${how}\:{we}\:{can}\:{convert}\:\mathrm{0}.\overset{−} {\mathrm{9}}\:{to}\:\frac{{q}}{{p}}? \\ $$
Question Number 128636 Answers: 1 Comments: 0
Question Number 128632 Answers: 0 Comments: 0
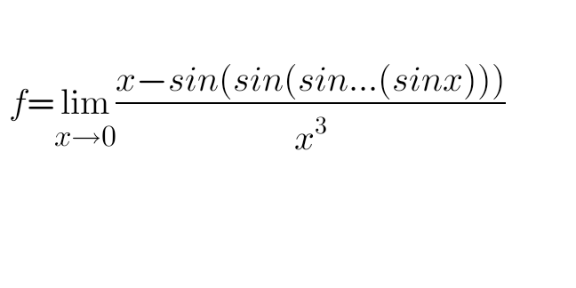
Question Number 128617 Answers: 1 Comments: 1
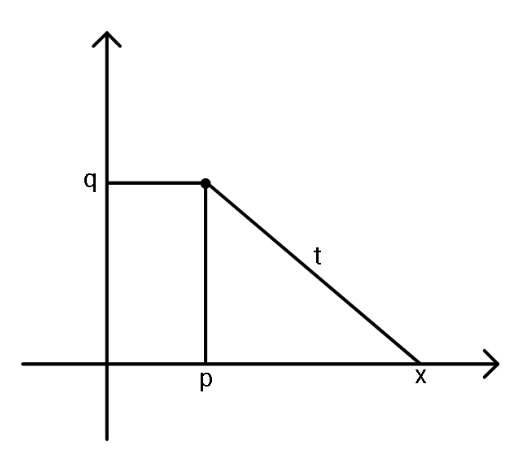
Question Number 128589 Answers: 1 Comments: 0
Question Number 128509 Answers: 1 Comments: 0

Question Number 128508 Answers: 1 Comments: 0
$${if}\:\:{x}^{{x}^{\mathrm{3}} } =\mathrm{3} \\ $$$${find}\:{x} \\ $$
Question Number 128457 Answers: 0 Comments: 1
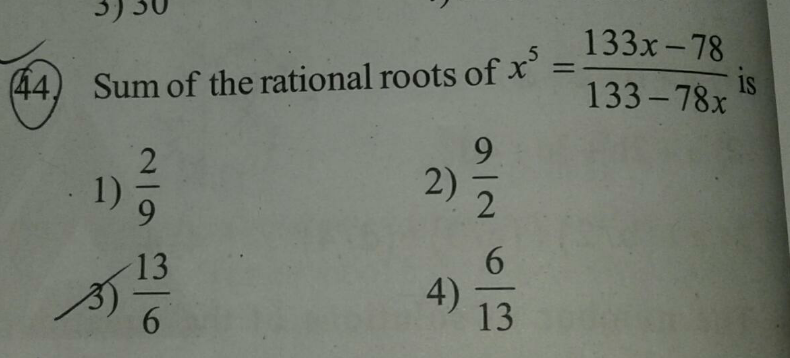
Question Number 128459 Answers: 1 Comments: 0
Question Number 128388 Answers: 0 Comments: 1
Question Number 128458 Answers: 0 Comments: 1

Question Number 128371 Answers: 1 Comments: 1
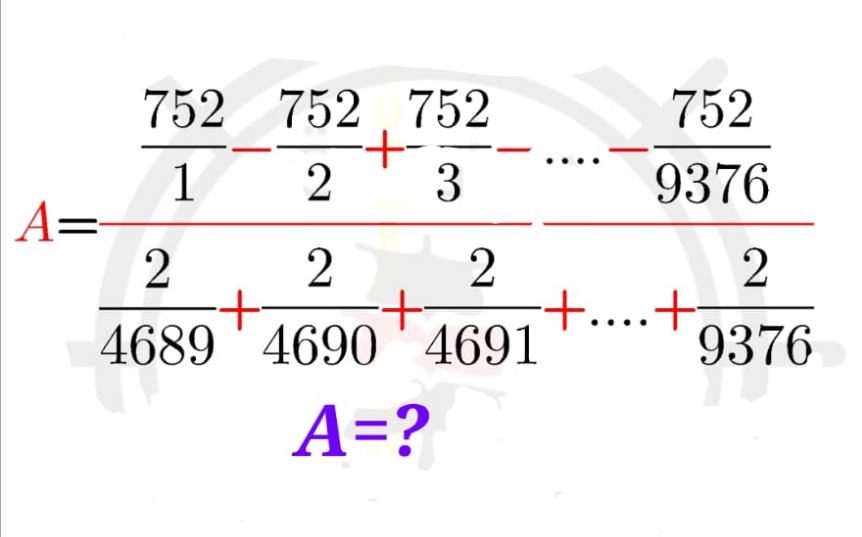
Question Number 128369 Answers: 2 Comments: 0
Question Number 128368 Answers: 2 Comments: 0
Question Number 128341 Answers: 1 Comments: 5
Question Number 128329 Answers: 2 Comments: 0
Question Number 128290 Answers: 0 Comments: 4
Question Number 128264 Answers: 1 Comments: 3
Question Number 128232 Answers: 0 Comments: 0
Question Number 128204 Answers: 0 Comments: 0
Question Number 128171 Answers: 0 Comments: 0

Question Number 128146 Answers: 1 Comments: 0
Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233
