
AlgebraQuestion and Answers: Page 227
Question Number 131158 Answers: 1 Comments: 0
Question Number 131155 Answers: 2 Comments: 0
Question Number 206939 Answers: 1 Comments: 7
In how many ways can the word KINECTIC be arranged so that no vowels can be together?
Question Number 131084 Answers: 2 Comments: 0
Question Number 131075 Answers: 1 Comments: 0
Question Number 131064 Answers: 3 Comments: 0
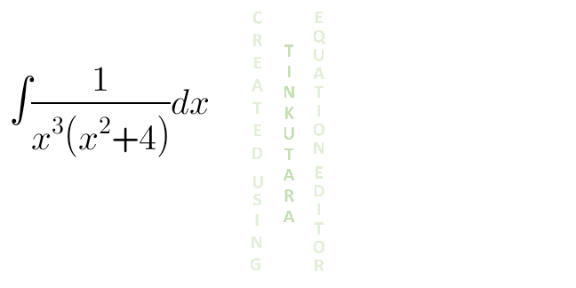
Question Number 131016 Answers: 0 Comments: 0
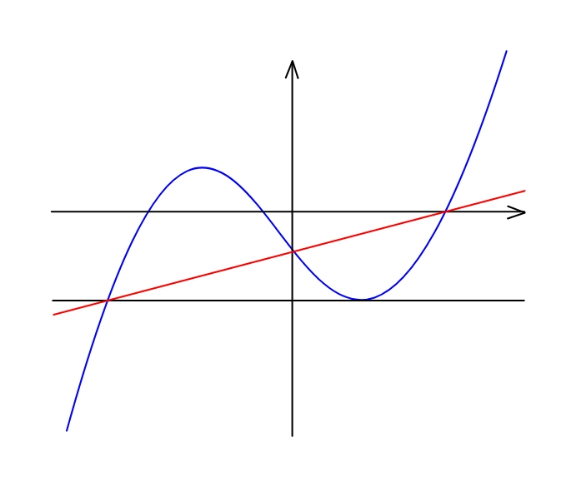
Question Number 130853 Answers: 1 Comments: 0
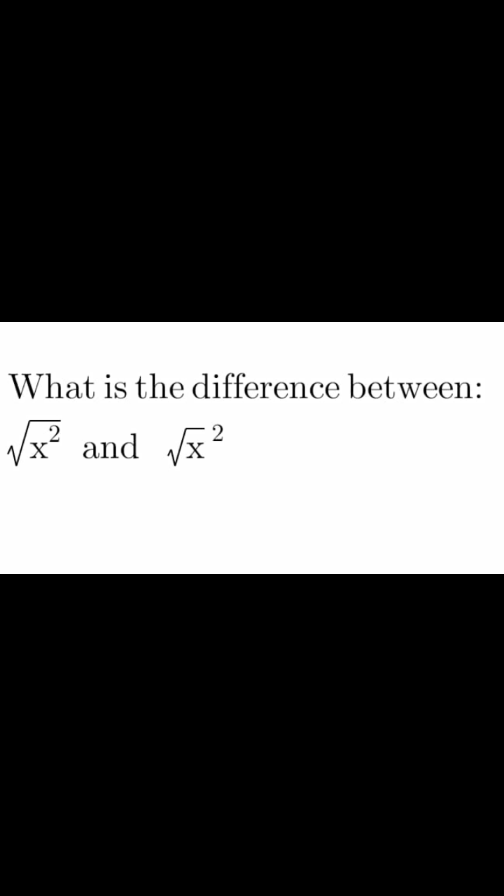
Question Number 130846 Answers: 1 Comments: 1
Question Number 130806 Answers: 1 Comments: 0
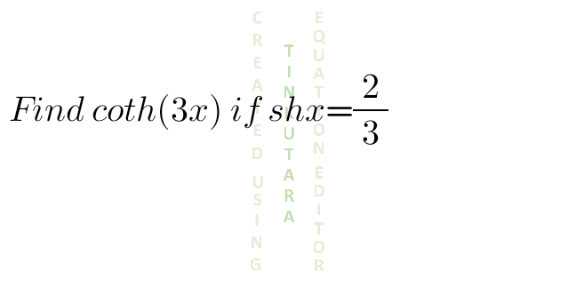
Question Number 130802 Answers: 2 Comments: 0
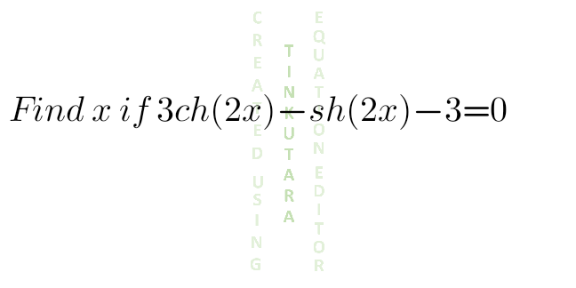
Question Number 130800 Answers: 0 Comments: 1

Question Number 130733 Answers: 1 Comments: 1

Question Number 130719 Answers: 0 Comments: 2
Question Number 130673 Answers: 0 Comments: 0

Question Number 130605 Answers: 2 Comments: 0
Question Number 130593 Answers: 1 Comments: 3
Question Number 130496 Answers: 3 Comments: 0
$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}!\right)=? \\ $$
Question Number 130476 Answers: 1 Comments: 0

Question Number 130472 Answers: 2 Comments: 0

Question Number 130455 Answers: 0 Comments: 0
Question Number 130442 Answers: 2 Comments: 0
Question Number 130426 Answers: 2 Comments: 0

Question Number 130383 Answers: 1 Comments: 0
$${If}\:\left({a}−\mathrm{2}\right)+\mathrm{3}{i}=\mathrm{5}−{bi}\:{then}\:{a}+{b}= \\ $$
Question Number 130362 Answers: 3 Comments: 0
Question Number 130354 Answers: 5 Comments: 0
Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231
