
AlgebraQuestion and Answers: Page 226
Question Number 133738 Answers: 3 Comments: 0

Question Number 133664 Answers: 1 Comments: 0
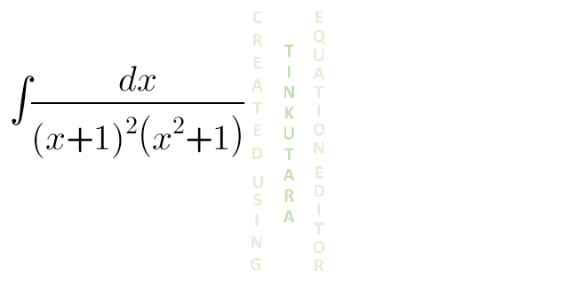
Question Number 133653 Answers: 1 Comments: 0
Question Number 133612 Answers: 0 Comments: 2
Question Number 133568 Answers: 2 Comments: 0
Question Number 133542 Answers: 0 Comments: 1

Question Number 133469 Answers: 1 Comments: 0
Question Number 133450 Answers: 0 Comments: 0
Question Number 133423 Answers: 1 Comments: 4

Question Number 133318 Answers: 1 Comments: 0
Question Number 133279 Answers: 0 Comments: 0
Question Number 133201 Answers: 2 Comments: 0
Question Number 133180 Answers: 1 Comments: 3

Question Number 133072 Answers: 1 Comments: 0
Question Number 133053 Answers: 1 Comments: 0
Question Number 133009 Answers: 1 Comments: 1
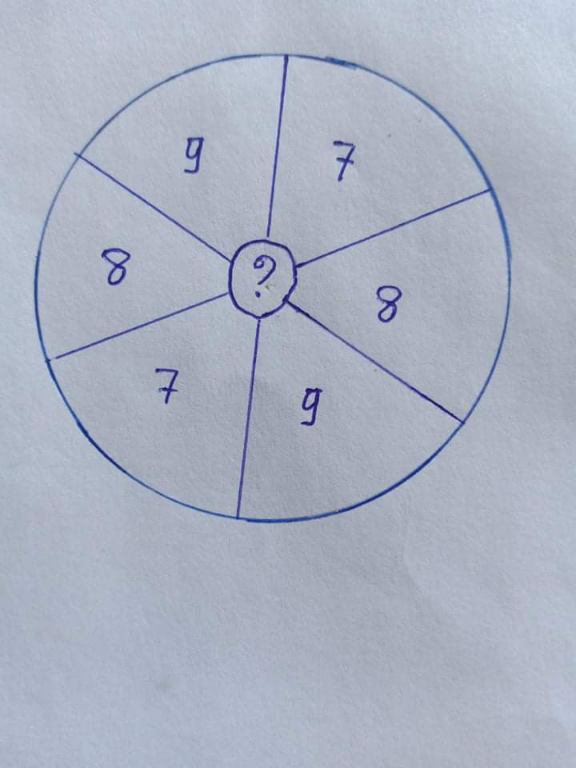
Question Number 132961 Answers: 1 Comments: 0

Question Number 132900 Answers: 0 Comments: 1
Question Number 132697 Answers: 3 Comments: 2
Question Number 132630 Answers: 0 Comments: 0

Question Number 132535 Answers: 1 Comments: 0

Question Number 132494 Answers: 2 Comments: 3

Question Number 132470 Answers: 2 Comments: 0
Question Number 132390 Answers: 1 Comments: 0
Question Number 132358 Answers: 0 Comments: 2
Question Number 132295 Answers: 0 Comments: 4

Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230
